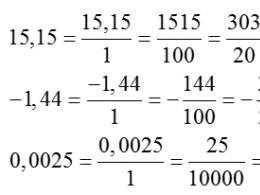Kümnendmurrud. Arvude teisendamine ühest numbrisüsteemist teise Internetis Selle video kommentaarid
Näib, et kümnendmurru teisendamine tavaliseks murruks on elementaarne teema, kuid paljud õpilased ei saa sellest aru! Seetõttu vaatleme täna üksikasjalikult mitut algoritmi korraga, mille abil mõistate mis tahes murde vaid sekundiga.
Lubage mul teile meelde tuletada, et sama murru kirjutamiseks on vähemalt kaks vormi: harilik ja kümnend. Kümnendmurrud on kõikvõimalikud konstruktsioonid kujul 0,75; 1,33; ja isegi −7,41. Siin on näited tavalistest murdudest, mis väljendavad samu numbreid:
Nüüd mõtleme välja: kuidas liikuda kümnendmärgistuselt tavalisele tähistusele? Ja mis kõige tähtsam: kuidas seda võimalikult kiiresti teha?
Põhialgoritm
Tegelikult on vähemalt kaks algoritmi. Ja me vaatame nüüd mõlemat. Alustame esimesest – kõige lihtsamast ja arusaadavamast.
Kümnendarvu teisendamiseks murdarvuks peate järgima kolme sammu:
Oluline märkus negatiivsete arvude kohta. Kui esialgses näites on kümnendmurru ees miinusmärk, siis väljundis peaks hariliku murru ees olema ka miinusmärk. Siin on veel mõned näited:
 Näiteid üleminekust murdude kümnendmärkimiselt tavalisele
Näiteid üleminekust murdude kümnendmärkimiselt tavalisele Tahaksin pöörata erilist tähelepanu viimasele näitele. Nagu näete, sisaldab murd 0,0025 pärast koma palju nulle. Selle tõttu tuleb lugeja ja nimetaja koguni neli korda korrutada 10. Kas sellisel juhul on võimalik algoritmi kuidagi lihtsustada?
Muidugi sa suudad. Ja nüüd vaatame alternatiivset algoritmi - seda on veidi keerulisem mõista, kuid pärast väikest harjutamist töötab see palju kiiremini kui tavaline.
Kiirem viis
Sellel algoritmil on samuti 3 sammu. Kümnendarvust murdosa saamiseks tehke järgmist.
- Loendage, mitu numbrit on pärast koma. Näiteks murdarvul 1,75 on kaks sellist numbrit ja 0,0025-l neli. Tähistame seda kogust tähega $n$.
- Kirjutage algne arv ümber murduna kujul $\frac(a)(((10)^(n)))$, kus $a$ on kõik algse murru numbrid (ilma "alguse" nullideta vasakule, kui see on olemas) ja $n$ on sama arv numbreid pärast koma, mille arvutasime esimeses etapis. Teisisõnu, peate jagama algse murru numbrid ühega, millele järgneb $n$ null.
- Võimalusel vähendage saadud fraktsiooni.
See on kõik! Esmapilgul on see skeem keerulisem kui eelmine. Kuid tegelikult on see nii lihtsam kui ka kiirem. Otsustage ise:
Nagu näete, on murdarvus 0,64 pärast koma kaks numbrit - 6 ja 4. Seega $n=2$. Kui eemaldame vasakult koma ja nullid (antud juhul vaid ühe nulli), saame arvu 64. Liigume edasi teise sammu juurde: $((10)^(n))=((10)^ (2))=100$, Seetõttu on nimetaja täpselt sada. No siis jääb üle ainult lugejat ja nimetajat vähendada. :)
Veel üks näide:
Siin on kõik veidi keerulisem. Esiteks on pärast koma juba 3 numbrit, st. $n=3$, seega tuleb jagada $((10)^(n))=((10)^(3))=1000$. Teiseks, kui eemaldada koma kümnendmärgistusest, saame järgmise: 0,004 → 0004. Pidage meeles, et vasakult nullid tuleb eemaldada, nii et tegelikult on meil arv 4. Siis on kõik lihtne: jagage, vähendage ja saage vastus.
Lõpuks viimane näide:
Selle murdosa eripära on terve osa olemasolu. Seetõttu on meie väljundiks vale murdosa 47/25. Muidugi võite proovida jagada 47 jäägiga 25-ga ja seega kogu osa uuesti eraldada. Aga miks teha oma elu keeruliseks, kui seda saab teha ümberkujundamise etapis? Noh, mõtleme välja.
Mida teha kogu osaga
Tegelikult on kõik väga lihtne: kui tahame saada õiget murdu, siis peame teisenduse käigus sellest kogu osa eemaldama ja siis, kui saame tulemuse, lisame selle uuesti paremale enne murrujoont. .
Näiteks kaaluge sama numbrit: 1,88. Hindame ühega (terve osa) ja vaatame murdosa 0,88. Seda saab hõlpsasti teisendada:
Seejärel meenutame "kadunud" üksust ja lisame selle esiküljele:
\[\frac(22)(25)\kuni 1\frac(22)(25)\]
See on kõik! Vastus osutus samaks, mis eelmisel korral terve osa välja valides. Paar näidet veel:
\[\begin(align)& 2.15\to 0.15=\frac(15)(100)=\frac(3)(20)\to 2\frac(3)(20); \\& 13,8\kuni 0,8=\frac(8)(10)=\frac(4)(5)\kuni 13\frac(4)(5). \\\lõpp(joonda)\]
See on matemaatika ilu: olenemata sellest, mis suunas sa lähed, kui kõik arvutused on õigesti tehtud, on vastus alati sama. :)
Kokkuvõtteks tahaksin kaaluda veel ühte tehnikat, mis aitab paljusid.
Teisendused "kõrva järgi"
Mõelgem, mis on koma isegi. Täpsemalt, kuidas me seda loeme. Näiteks arv 0,64 – me loeme seda "null koma 64 sajandikku", eks? Noh, või lihtsalt "64 sajandikku". Võtmesõnaks on siinkohal “sajandikud”, st. number 100.
Aga 0,004? See on "null koma 4 tuhandikku" või lihtsalt "neli tuhandikku". Nii või teisiti on märksõnaks “tuhanded”, s.t. 1000.
Mis on siis suur asi? Ja tõsiasi on see, et just need numbrid "hüppavad" lõpuks nimetajates algoritmi teises etapis. Need. 0,004 on "neli tuhandikku" või "4 jagatud 1000-ga":
Proovige ise harjutada – see on väga lihtne. Peaasi on algset murdu õigesti lugeda. Näiteks 2,5 on "2 tervet, 5 kümnendikku", nii et
Ja mingi 1,125 on "1 tervik, 125 tuhandikku", nii et
Viimases näites vaidleb keegi muidugi vastu, et igale õpilasele ei ole ilmne, et 1000 jagub 125-ga. Kuid siin tuleb meeles pidada, et 1000 = 10 3 ja 10 = 2 ∙ 5, seega
\[\begin(align)& 1000=10\cdot 10\cdot 10=2\cdot 5\cdot 2\cdot 5\cdot 2\cdot 5= \\& =2\cdot 2\cdot 2\cdot 5\ cdot 5\cdot 5=8\cdot 125\end(joonda)\]
Seega jaotatakse iga kümne aste ainult teguriteks 2 ja 5 - just neid tegureid tuleb lugejast otsida, et lõpuks kõik väheneks.
Sellega õppetund lõpeb. Liigume edasi keerukama pöördoperatsiooni juurde - vt "
Juhtub, et arvutuste mugavuse huvides peate teisendama tavalise murdarvu kümnendkohaks ja vastupidi. Sellest, kuidas seda teha, räägime selles artiklis. Vaatame tavaliste murdude kümnendkohtadeks teisendamise reegleid ja vastupidi ning toome ka näiteid.
Yandex.RTB R-A-339285-1
Kaalume tavaliste murdude teisendamist kümnendkohtadeks, järgides teatud järjestust. Kõigepealt vaatame, kuidas teisendatakse tavalised murded, mille nimetaja on 10-kordne: 10, 100, 1000 jne. Sellise nimetajaga murrud on tegelikult kümnendmurdude tülikam märkimine.
Järgmisena vaatleme, kuidas teisendada mis tahes nimetajaga tavalisi murde, mitte ainult 10 kordajaid, kümnendmurrudeks. Pange tähele, et tavaliste murdude kümnendmurrudeks teisendamisel saadakse mitte ainult lõplikud kümnendmurrud, vaid ka lõpmatud perioodilised kümnendmurrud.
Alustame!
Harilike murdude tõlkimine nimetajatega 10, 100, 1000 jne. kümnendkohtadeni
Esiteks oletame, et mõned murrud nõuavad enne kümnendvormiks teisendamist ettevalmistamist. Mis see on? Enne lugejas olevat numbrit peate lisama nii palju nulle, et lugeja numbrite arv oleks võrdne nimetaja nullide arvuga. Näiteks murdarvu 3100 puhul tuleb number 0 lisada üks kord lugejas olevast 3-st vasakule. Fraktsioon 610 ei vaja vastavalt ülaltoodud reeglile muutmist.
Vaatame veel ühte näidet, mille järel sõnastame reegli, mida on alguses eriti mugav kasutada, samas kui murdude teisendamisel pole palju kogemusi. Seega näeb murdosa 1610000 pärast nullide lisamist lugejasse välja nagu 001510000.
Kuidas teisendada harilikku murru nimetajaga 10, 100, 1000 jne. kümnendkohani?
Reegel tavaliste pärismurdude kümnendkohtadeks teisendamiseks
- Kirjutage 0 ja pange selle järele koma.
- Lugejast kirjutame üles numbri, mis saadi pärast nullide lisamist.
Liigume nüüd näidete juurde.
Näide 1: Murdude teisendamine kümnendkohtadeks
Teisendame murdarvu 39 100 kümnendkohaks.
Esiteks vaatame murdosa ja näeme, et mingeid ettevalmistavaid toiminguid pole vaja teha - lugeja numbrite arv langeb kokku nimetaja nullide arvuga.
Reegli järgi kirjutame 0, paneme selle järele koma ja kirjutame lugejast numbri. Saame kümnendmurruks 0,39.
Vaatame veel ühe selleteemalise näite lahendust.
Näide 2. Murdude teisendamine kümnendkohtadeks
Kirjutame murdarvu 105 10000000 kümnendkohana.
Nullide arv nimetajas on 7 ja lugejas on ainult kolm numbrit. Lisame lugejas oleva numbri ette veel 4 nulli:
0000105 10000000
Nüüd kirjutame üles 0, paneme selle järele koma ja kirjutame numbri lugejast üles. Saame kümnendmurruks 0,0000105.
Kõikides näidetes käsitletavad murded on tavalised õiged murded. Aga kuidas teisendada vale murd kümnendkohaks? Ütleme kohe, et selliste murdude jaoks pole nullide lisamisega ettevalmistust vaja. Sõnastame reegli.
Reegel tavaliste ebaõigete murdude kümnendkohtadeks teisendamiseks
- Kirjutage üles number, mis on lugejas.
- Kasutame koma, et eraldada paremal pool nii palju nulle, kui palju on algmurru nimetajas nulle.
Allpool on näide selle reegli kasutamise kohta.
Näide 3. Murdude teisendamine kümnendkohtadeks
Teisendame murru 56888038009 100000 tavalisest ebakorrapärasest murrust kümnendkohaks.
Kõigepealt kirjutame lugejast numbri üles:
Nüüd eraldame paremal viis numbrit kümnendkohaga (nullide arv nimetajas on viis). Saame:
Järgmine loomulikult kerkib küsimus: kuidas teisendada segaarv kümnendmurruks, kui selle murdosa nimetajaks on arv 10, 100, 1000 jne. Sellise arvu kümnendmurruks teisendamiseks võite kasutada järgmist reeglit.
Segaarvude kümnendkohtadeks teisendamise reegel
- Vajadusel valmistame ette arvu murdosa.
- Kirjutame üles kogu algnumbri osa ja paneme selle järele koma.
- Kirjutame murdosa lugejast numbri üles koos lisatud nullidega.
Vaatame näidet.
Näide 4: segaarvude teisendamine kümnendkohtadeks
Teisendame segaarvu 23 17 10000 kümnendmurruks.
Murdosas on avaldis 17 10000. Valmistame selle ette ja lisame lugejast vasakule veel kaks nulli. Saame: 0017 10000.
Nüüd kirjutame kogu arvu osa üles ja paneme selle järele koma: 23, . .
Pärast koma kirjutage lugejast number koos nullidega üles. Saame tulemuse:
23 17 10000 = 23 , 0017
Harilike murdude teisendamine lõplikeks ja lõpmatuteks perioodilisteks murdudeks
Loomulikult saate teisendada kümnendkohtadeks ja tavalisteks murdudeks, mille nimetaja ei ole 10, 100, 1000 jne.
Sageli saab murdosa hõlpsasti taandada uueks nimetajaks ja seejärel kasutada selle artikli esimeses lõigus sätestatud reeglit. Näiteks piisab, kui korrutada murdarvu 25 lugeja ja nimetaja 2-ga ning saame murdarvu 410, mis teisendatakse kergesti kümnendvormiks 0,4.
Seda murdarvu kümnendkohaks teisendamise meetodit ei saa aga alati kasutada. Allpool kaalume, mida teha, kui vaadeldavat meetodit pole võimalik rakendada.
Põhimõtteliselt uus viis murdarvu kümnendkohaks teisendamiseks on jagada lugeja veeruga nimetajaga. See toiming on väga sarnane naturaalarvude jagamisele veeruga, kuid sellel on oma omadused.
Jagamisel esitatakse lugeja kümnendmurruna - lugeja viimasest numbrist paremale pannakse koma ja lisatakse nullid. Saadud jagatis asetatakse koma, kui lugeja täisarvu osa jagamine lõpeb. Kuidas see meetod täpselt töötab, selgub pärast näidete vaatamist.
Näide 5. Murdude teisendamine kümnendkohtadeks
Teisendame hariliku murru 621 4 kümnendvormingusse.
Esitame arvu 621 lugejast kümnendmurruna, lisades pärast koma paar nulli. 621 = 621,00
Nüüd jagame 621,00 veeru abil 4-ga. Jagamise kolm esimest sammu on samad, mis naturaalarvude jagamisel ja me saame.
Kui jõuame dividendis komakohani ja jääk erineb nullist, paneme jagatisesse koma ja jätkame jagamist, pööramata enam tähelepanu komale dividendis.

Selle tulemusena saame kümnendmurru 155, 25, mis on hariliku murru 621 4 ümberpööramise tulemus
621 4 = 155 , 25
Vaatame materjali tugevdamiseks teist näidet.
Näide 6. Murdude teisendamine kümnendkohtadeks
Pöörame hariliku murru 21 800 ümber.
Selleks jagage murdosa 21 000 veergu 800-ga. Kogu osa jagamine lõpeb esimese sammuga, nii et kohe pärast seda paneme jagatisesse koma ja jätkame jagamist, pööramata tähelepanu komale dividendis, kuni saame nulliga võrdse jäägi.

Selle tulemusena saime: 21 800 = 0,02625.
Aga mis siis, kui jagamisel ei saa me ikkagi jääki 0. Sellistel juhtudel võib jagamist jätkata lõputult. Kuid alates teatud etapist korratakse jääke perioodiliselt. Vastavalt sellele korratakse jagatis olevaid numbreid. See tähendab, et harilik murd teisendatakse kümnendmurruks lõpmatuks perioodiliseks murdeks. Illustreerime seda näitega.
Näide 7. Murdude teisendamine kümnendkohtadeks
Teisendame hariliku murru 19 44 kümnendkohaks. Selleks teostame veergude kaupa jagamise.

Näeme, et jagamisel korduvad jäägid 8 ja 36. Sel juhul korduvad numbrid 1 ja 8 jagatis. See on periood kümnendmurrus. Salvestamise ajal pannakse need numbrid sulgudesse.
Seega teisendatakse algne harilik murd lõpmatuks perioodiliseks kümnendmurruks.
19 44 = 0 , 43 (18) .
Vaatame taandamatut harilikku murru. Mis vormi see võtab? Millised harilikud murrud teisendatakse lõplikeks kümnendkohtadeks ja millised lõpmatuteks perioodilisteks?
Esiteks oletame, et kui murdosa saab taandada ühele nimetajatest 10, 100, 1000..., siis on see lõpliku kümnendmurru kujul. Selleks, et murdosa taandataks ühele neist nimetajatest, peab selle nimetaja olema vähemalt ühe arvu 10, 100, 1000 jne jagaja. Arvude algteguriteks faktooringu reeglitest järeldub, et arvude jagaja on 10, 100, 1000 jne. kui algteguritesse arvesse võtta, peab see sisaldama ainult numbreid 2 ja 5.
Võtame öeldu kokku:
- Harilikku murru saab taandada viimase kümnendkohani, kui selle nimetaja saab arvesse võtta algteguriteks 2 ja 5.
- Kui nimetaja laienduses on lisaks arvudele 2 ja 5 ka teisi algarve, taandatakse murd lõpmatu perioodilise kümnendmurru kujule.
Toome näite.
Näide 8. Murdude teisendamine kümnendkohtadeks
Milline neist murdudest 47 20, 7 12, 21 56, 31 17 teisendatakse lõplikuks kümnendmurruks ja milline - ainult perioodiliseks. Vastame sellele küsimusele ilma murdosa kümnendkohaks teisendamata.
Murd 47 20, nagu on lihtne näha, taandatakse lugeja ja nimetaja 5-ga korrutamisel uueks nimetajaks 100.
47 20 = 235 100. Sellest järeldame, et see murdosa teisendatakse lõplikuks kümnendmurruks.
Murru 7 12 nimetaja faktoriseerimine annab 12 = 2 · 2 · 3. Kuna algtegur 3 erineb 2-st ja 5-st, ei saa seda murdu esitada lõpliku kümnendmurruna, vaid sellel on lõpmatu perioodiline murd.
Esiteks tuleb murdosa 21 56 vähendada. Pärast 7-ga taandamist saame taandamatu murdosa 3 8, mille nimetaja faktoriseeritakse, et saada 8 = 2 · 2 · 2. Seetõttu on see viimane kümnendmurd.
Murru 31 17 puhul on nimetaja faktoriseerimine algarv 17 ise. Sellest tulenevalt saab selle murdosa teisendada lõpmatuks perioodiliseks kümnendmurruks.
Tavalist murdu ei saa teisendada lõpmatuks ja mitteperioodiliseks kümnendmurruks
Eespool rääkisime ainult lõplikest ja lõpmatutest perioodilistest murdudest. Kuid kas mis tahes harilikku murdu saab teisendada lõpmatuks mitteperioodiliseks murdeks?
Vastame: ei!
Tähtis!
Kui teisendada lõpmatu murd kümnendkohaks, on tulemuseks kas lõplik koma või lõpmatu perioodiline kümnendkoht.
Jaotuse ülejäänud osa on alati väiksem kui jagaja. Ehk jaguvuse teoreemi järgi, kui jagada mingi naturaalarv arvuga q, siis jagamise jääk ei saa igal juhul olla suurem kui q-1. Pärast jagamise lõpetamist on võimalik üks järgmistest olukordadest:
- Saame jäägi 0 ja sellega jagamine lõpeb.
- Saame jäägi, mida korratakse järgneval jagamisel, mille tulemuseks on lõpmatu perioodiline murd.
Murru kümnendkohaks teisendamisel ei saa olla muid võimalusi. Ütleme ka, et perioodi pikkus (numbrite arv) lõpmatus perioodilises murrus on alati väiksem kui vastava hariliku murru nimetaja numbrite arv.
Kümnendkohtade teisendamine murdudeks
Nüüd on aeg vaadata kümnendmurru harilikuks murruks teisendamise vastupidist protsessi. Sõnastame tõlkereegli, mis sisaldab kolme etappi. Kuidas teisendada kümnendmurru harilikuks murruks?
Kümnendmurdude harilikeks murdudeks teisendamise reegel
- Lugejasse kirjutame arvu algsest kümnendmurdust, jättes kõrvale koma ja kõik vasakul olevad nullid, kui neid on.
- Nimetajasse kirjutame ühe, millele järgneb nii palju nulle, kui palju on koma pärast esialgses kümnendmurrus numbreid.
- Vajadusel vähendage saadud harilikku fraktsiooni.
Vaatame selle reegli rakendamist näidete abil.
Näide 8. Kümnendmurdude teisendamine tavalisteks murdudeks
Kujutagem ette arvu 3,025 tavalise murruna.
- Kirjutame kümnendmurru enda lugejasse, jättes koma kõrvale: 3025.
- Nimetajasse kirjutame ühe ja selle järele kolm nulli - täpselt nii palju numbrit sisaldub algses murrus pärast koma: 3025 1000.
- Saadud murdosa 3025 1000 saab vähendada 25 võrra, mille tulemuseks on: 3025 1000 = 121 40.
Näide 9. Kümnendmurdude teisendamine tavalisteks murdudeks
Teisendame murdarvu 0,0017 kümnendkohast tavaliseks.
- Lugejasse kirjutame murdosa 0, 0017, jättes kõrvale vasakul olevad koma ja nullid. Selgub, et 17.
- Nimetajasse kirjutame ühe ja selle järele neli nulli: 17 10000. See murdosa on taandamatu.
Kui kümnendmurrul on täisarvuline osa, siis saab sellise murru kohe teisendada segaarvuks. Kuidas seda teha?
Sõnastame veel ühe reegli.
Reegel kümnendarvude teisendamiseks segaarvudeks.
- Arv enne koma murdosas kirjutatakse segaarvu täisarvuna.
- Lugejas kirjutame arvu murdosas pärast koma, jättes kõrvale vasakul olevad nullid, kui neid on.
- Murdosa nimetajasse liidame ühe ja nii palju nulle, kui palju on murdosa koma järel numbreid.
Võtame näite
Näide 10. Kümnendarvu teisendamine segaarvuks
Kujutagem ette murdarvu 155, 06005 segaarvuna.
- Arvu 155 kirjutame täisarvulise osana.
- Lugejas kirjutame numbrid pärast koma, jättes nulli kõrvale.
- Nimetajasse kirjutame ühe ja viis nulli
Õpime selgeks segaarvu: 155 6005 100 000
Murdosa saab vähendada 5 võrra. Lühendame seda ja saame lõpptulemuse:
155 , 06005 = 155 1201 20000
Lõpmatu arvu perioodiliste kümnendkohtade teisendamine murdudeks
Vaatame näiteid perioodiliste kümnendmurrude teisendamiseks tavalisteks murdudeks. Enne kui alustame, teeme selgeks: iga perioodilise kümnendmurru saab teisendada tavaliseks murruks.
Lihtsaim juhtum on siis, kui murdosa periood on null. Perioodiline nullpunktiga murd asendatakse lõpliku kümnendmurruga ja sellise murru ümberpööramise protsess taandatakse viimase kümnendmurru ümberpööramiseks.
Näide 11. Perioodilise kümnendmurru teisendamine harilikuks murruks
Inverteerime perioodilise murru 3, 75 (0).
Parempoolsed nullid kõrvaldades saame viimase kümnendmurru 3,75.
Teisendades selle murdosa tavaliseks murruks, kasutades eelmistes lõikudes käsitletud algoritmi, saame:
3 , 75 (0) = 3 , 75 = 375 100 = 15 4 .
Mis siis, kui murdosa periood erineb nullist? Perioodilist osa tuleks käsitleda geomeetrilise progressiooni liikmete summana, mis väheneb. Selgitame seda näitega:
0 , (74) = 0 , 74 + 0 , 0074 + 0 , 000074 + 0 , 00000074 + . .
Lõpmatult kahaneva geomeetrilise progressiooni liikmete summa jaoks on olemas valem. Kui progressiooni esimene liige on b ja nimetaja q on selline, et 0< q < 1 , то сумма равна b 1 - q .
Vaatame selle valemi abil mõnda näidet.
Näide 12. Perioodilise kümnendmurru teisendamine harilikuks murruks
Olgu meil perioodiline murd 0, (8) ja see tuleb teisendada tavaliseks.
0 , (8) = 0 , 8 + 0 , 08 + 0 , 008 + . .
Siin on lõpmatult kahanev geomeetriline progressioon, mille esimene liige on 0, 8 ja nimetaja 0, 1.
Rakendame valemit:
0 , (8) = 0 , 8 + 0 , 08 + 0 , 008 + . . = 0 , 8 1 - 0 , 1 = 0 , 8 0 , 9 = 8 9
See on vajalik harilik murd.
Materjali konsolideerimiseks kaaluge teist näidet.
Näide 13. Perioodilise kümnendmurru teisendamine harilikuks murruks
Pöörame murdosa 0, 43 (18) ümber.
Kõigepealt kirjutame murdosa lõpmatu summana:
0 , 43 (18) = 0 , 43 + (0 , 0018 + 0 , 000018 + 0 , 00000018 . .)
Vaatame sulgudes olevaid termineid. Seda geomeetrilist progressiooni saab esitada järgmiselt:
0 , 0018 + 0 , 000018 + 0 , 00000018 . . = 0 , 0018 1 - 0 , 01 = 0 , 0018 0 , 99 = 18 9900 .
Lisame tulemuse lõplikule murdarvule 0, 43 = 43 100 ja saame tulemuse:
0 , 43 (18) = 43 100 + 18 9900
Pärast nende murdude lisamist ja vähendamist saame lõpliku vastuse:
0 , 43 (18) = 19 44
Selle artikli lõpetuseks ütleme, et mitteperioodilisi lõpmatuid kümnendmurde ei saa teisendada tavalisteks murdudeks.
Kui märkate tekstis viga, tõstke see esile ja vajutage Ctrl+Enter
Üsna sageli nõutakse matemaatikas murdarvu teisendamist kümnendkohaks. Selle põhjuseks on eelkõige asjaolu, et kümnendmurrud on omamoodi üldtunnustatud standard ja neid kasutatakse sagedamini kui tavalisi murde. Näiteks riigieksami blankettidele on lubatud kirjutada ainult kümnendmurde. Või me ei ütle poes: "Anna mulle teine kolm kilogrammi suhkrut."
Kuidas teisendada murd kümnendkohaks
Lihtmurru kümnendkohaks teisendamiseks vajate jagama lugeja peal nimetaja (murrurea kohal olev arv selle all oleva numbri võrra). Vaatleme mitut võimalikku juhtumit.
- Juhtum 1. Meil on lihtne õige murd (<1) Возьмем заданную дробь (1 / 2) и переведем ее в десятичную. Для удобства можно выполнить деление столбиком (или калькулятором). Делим 1 на 2 и получаем 0,5.
- Juhtum 2. Meil on vale murd (>1) või meil on täisarvuline osa. Me ei puuduta tervet osa, aga kui seda saab valida, siis valime selle. Näiteks 3/2 = 1 1/2. Lahkume üksusest ja murdosaga teostame meile juba teadaolevaid toiminguid. Vastus on 1,5.
- Juhtum 3. Jagamisel me lõplikku arvu ei saa ehk vastuseks on lõpmatu kümnendmurd. On kaks võimalust. 1) Kui murdosa osutub perioodiliseks (0,6666...), siis saab vastuse kirjutada järgmiselt: 0,(6) . 2) Kui murdosa ei ole perioodiline, saame arvu ümardada suvaliseks arvuks (kümnendikuteks, sajandikuteks), kui ainult tingimus seda võimaldab. Kui ei, siis on parem jätta arv lihtmurruna.
Murru kümnendkohaks teisendamiseks peate teisendama murdosa nimetaja 10-ks, 100-ks, 1000-ks jne. Näiteks teisendame murdosa 1/2:
1. Esimese sammuna tuleb leida täisarv, mis teisendab nimetaja 10, 100, 1000 jne. Selleks jagame vaheldumisi loendis olevaid numbreid (10, 100, 1000) nimetajaga, kuni saame täisarvu.
10/2 = 5 – täisarv;
1. Nüüd, korrutades oma murdosa saadud arvuga (5), teisendame oma murdarvu kümnendkohaks.
Anonüümne
Murru kümnendkohaks teisendamiseks peate teisendama murdosa nimetaja 10-ks, 100-ks, 1000-ks jne. Näitena teisendame murdosa 1/2: 1. Esimese sammuna tuleb leida täisarv, mis teisendab nimetaja 10, 100, 1000 jne. Selleks jagame vaheldumisi loendis olevaid numbreid (10, 100, 1000) nimetajaga, kuni saame täisarvu. 10/2 = 5 – täisarv; 1. Nüüd, korrutades oma murdosa saadud arvuga (5), teisendame oma murdarvu kümnendkohaks. (1*5)/(2*5) = 5/10 = 0,5.
Anonüümne
Sissejuhatus
Üsna sageli nõutakse matemaatikas murdarvu teisendamist kümnendkohaks. Selle põhjuseks on eelkõige asjaolu, et kümnendmurrud on omamoodi üldtunnustatud standard ja neid kasutatakse sagedamini kui tavalisi murde. Näiteks riigieksami blankettidele on lubatud kirjutada ainult kümnendmurde. Või me ei ütle poes: "Anna mulle teine kolm kilogrammi suhkrut."
Kuidas teisendada murd kümnendkohaks
Lihtmurru kümnendkohaks teisendamiseks vajate jagama lugeja peal nimetaja (murrurea kohal olev arv selle all oleva numbri võrra). Vaatleme mitut võimalikku juhtumit.
- Juhtum 1. Meil on lihtne õige murd (<1) Возьмем заданную дробь (1 / 2) и переведем ее в десятичную. Для удобства можно выполнить деление столбиком (или калькулятором). Делим 1 на 2 и получаем 0,5.
- Juhtum 2. Meil on vale murd (>1) või meil on täisarvuline osa. Me ei puuduta tervet osa, aga kui seda saab valida, siis valime selle. Näiteks 3/2 = 1 1/2. Lahkume üksusest ja murdosaga teostame meile juba teadaolevaid toiminguid. Vastus on 1,5.
- Juhtum 3. Jagamisel me lõplikku arvu ei saa ehk vastuseks on lõpmatu kümnendmurd. On kaks võimalust. 1) Kui murdosa osutub perioodiliseks (0,6666...), siis saab vastuse kirjutada järgmiselt: 0,(6) . 2) Kui murdosa ei ole perioodiline, saame arvu ümardada suvaliseks arvuks (kümnendikuteks, sajandikuteks), kui ainult tingimus seda võimaldab. Kui ei, siis on parem jätta arv lihtmurruna.
Selle veebikalkulaatori abil saate teisendada täis- ja murdarvu ühest numbrisüsteemist teise. Antakse üksikasjalik lahendus koos selgitustega. Tõlkimiseks sisestage originaalarv, määrake lähtenumbri numbrisüsteemi alus, määrake numbrisüsteemi alus, millesse soovite numbri teisendada ja klõpsake nuppu "Tõlgi". Vaata teoreetilist osa ja numbrilisi näiteid allpool.
Tulemus on juba käes!
Täisarvude ja murdude teisendamine ühest arvusüsteemist teise - teooria, näited ja lahendused
On positsioonilisi ja mittepositsioonilisi arvusüsteeme. Araabia numbrisüsteem, mida me igapäevaelus kasutame, on positsiooniline, kuid rooma numbrisüsteem mitte. Positsioonilistes arvusüsteemides määrab arvu asukoht üheselt arvu suuruse. Vaatleme seda arvu 6372 näitel kümnendarvude süsteemis. Nummerdame selle numbri paremalt vasakule alustades nullist:
Siis saab numbrit 6372 esitada järgmiselt:
6372=6000+300+70+2 =6·10 3 +3·10 2 +7·10 1 +2·10 0 .
Arv 10 määrab numbrisüsteemi (antud juhul on see 10). Antud arvu asukoha väärtused võetakse astmetena.
Mõelge tegelikule kümnendarvule 1287,923. Nummerdame selle alustades nullist, arvu asukoht komakohast vasakule ja paremale:
Siis saab arvu 1287.923 esitada järgmiselt:
1287,923 =1000+200+80 +7+0,9+0,02+0,003 = 1·10 3 +2·10 2 +8·10 1 +7·10 0 +9·10-1 +2·10-2 +3· 10 -3.
Üldiselt võib valemit esitada järgmiselt:
C n s n +C n-1 · s n-1 +...+C 1 · s 1 +C 0 ·s 0 +D -1 ·s -1 +D -2 ·s -2 +...+D -k ·s -k
kus C n on positsiooni täisarv n, D -k - murdarv positsioonis (-k), s- numbrisüsteem.
Paar sõna arvusüsteemidest Kümnendarvusüsteemis koosneb arv paljudest numbritest (0,1,2,3,4,5,6,7,8,9), kaheksandarvusüsteemis paljudest numbritest (0,1, 2,3,4,5,6,7), kahendarvusüsteemis - numbrite hulgast (0,1), kuueteistkümnendsüsteemis - numbrite hulgast (0,1 ,2,3,4,5,6, 7,8,9,A,B,C,D,E,F), kus A,B,C,D,E,F vastavad numbritele 10,11, 12,13,14,15.Tabelis Tab.1 on numbrid esitatud erinevates numbrisüsteemides.
| Tabel 1 | |||
|---|---|---|---|
| Märge | |||
| 10 | 2 | 8 | 16 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E | 15 | 1111 | 17 | F |
Arvude teisendamine ühest numbrisüsteemist teise
Arvude teisendamiseks ühest arvusüsteemist teise on lihtsaim viis teisendada arv esmalt kümnendarvusüsteemi ja seejärel teisendada kümnendarvusüsteemist nõutavasse arvusüsteemi.
Arvude teisendamine mis tahes arvusüsteemist kümnendarvusüsteemi
Valemi (1) abil saate teisendada numbreid mis tahes arvusüsteemist kümnendarvude süsteemiks.
Näide 1. Teisendage arv 1011101.001 kahendarvusüsteemist (SS) kümnendarvuks SS. Lahendus:
1 ·2 6 +0 · 2 5 + 1 ·2 4+ 1 ·2 3+ 1 ·2 2+ 0 ·2 1+ 1 ·2 0+ 0 ·2 -1 + 0 ·2 -2 + 1 ·2 -3 =64+16+8+4+1+1/8=93,125
Näide2. Teisendage arv 1011101.001 kaheksandarvusüsteemist (SS) kümnendarvuks SS. Lahendus:
Näide 3 . Teisendage arv AB572.CDF kuueteistkümnendsüsteemist kümnendsüsteemi SS-i. Lahendus:
Siin A- asendatud 10-ga, B- kell 11, C- kell 12, F- 15-ks.
Arvude teisendamine kümnendarvusüsteemist teise arvusüsteemi
Arvude teisendamiseks kümnendarvusüsteemist teise arvusüsteemi tuleb teisendada arvu täisarvuline osa ja arvu murdosa eraldi.
Arvu täisarvuline osa teisendatakse kümnendarvust SS-st teise numbrisüsteemi, jagades arvu täisarvu osa numbrisüsteemi alusega (binaarse SS-i puhul - 2-ga, 8-kordse SS-i korral - 8-ga, 16-ga -ary SS - 16 võrra jne), kuni saadakse kogu jääk, mis on väiksem kui baas-CC.
Näide 4 . Teisendame arvu 159 kümnend-SS-st binaarseks SS-ks:
| 159 | 2 | ||||||
| 158 | 79 | 2 | |||||
| 1 | 78 | 39 | 2 | ||||
| 1 | 38 | 19 | 2 | ||||
| 1 | 18 | 9 | 2 | ||||
| 1 | 8 | 4 | 2 | ||||
| 1 | 4 | 2 | 2 | ||||
| 0 | 2 | 1 | |||||
| 0 |
Nagu näha jooniselt fig. 1, annab arv 159 2-ga jagamisel jagatise 79 ja jääk 1. Lisaks annab arv 79 2-ga jagamisel jagatise 39 ja jääk 1 jne. Selle tulemusel, konstrueerides arvu jagamisjääkidest (paremalt vasakule), saame binaarses SS-s arvu: 10011111 . Seetõttu võime kirjutada:
159 10 =10011111 2 .
Näide 5 . Teisendame arvu 615 kümnend-SS-st kaheksand-SS-ks.
| 615 | 8 | ||
| 608 | 76 | 8 | |
| 7 | 72 | 9 | 8 |
| 4 | 8 | 1 | |
| 1 |
Kui teisendate arvu kümnend-SS-st oktaalseks SS-ks, peate arvu jagama järjestikku 8-ga, kuni saate täisarvjäägi, mis on väiksem kui 8. Selle tulemusel saame jagamisjääkidest (paremalt vasakule) arvu konstrueerides. number kaheksand-SS-s: 1147 (vt joonis 2). Seetõttu võime kirjutada:
615 10 =1147 8 .
Näide 6 . Teisendame arvu 19673 kümnendarvusüsteemist kuueteistkümnendsüsteemi SS-ks.
| 19673 | 16 | ||
| 19664 | 1229 | 16 | |
| 9 | 1216 | 76 | 16 |
| 13 | 64 | 4 | |
| 12 |
Nagu on näha jooniselt 3, jagades arvu 19673 järjestikku 16-ga, on jäägid 4, 12, 13, 9. Kuueteistkümnendsüsteemis vastab arv 12 C-le, arv 13 D-le. Seetõttu on meie kuueteistkümnendsüsteem on 4CD9.
Tavaliste kümnendmurdude (null-täisarvuga reaalarvu) teisendamiseks alusega s arvusüsteemiks on vaja seda arvu järjestikku korrutada s-ga, kuni murdosa sisaldab puhast nulli või saame vajaliku arvu numbreid . Kui korrutamise käigus saadakse arv, mille täisarvuline osa on erinev nullist, siis seda täisarvu ei võeta arvesse (need kaasatakse tulemusesse järjestikku).
Vaatame ülaltoodut näidetega.
Näide 7 . Teisendame arvu 0,214 kümnendarvusüsteemist kahendarvuks SS.
| 0.214 | ||
| x | 2 | |
| 0 | 0.428 | |
| x | 2 | |
| 0 | 0.856 | |
| x | 2 | |
| 1 | 0.712 | |
| x | 2 | |
| 1 | 0.424 | |
| x | 2 | |
| 0 | 0.848 | |
| x | 2 | |
| 1 | 0.696 | |
| x | 2 | |
| 1 | 0.392 |
Nagu on näha jooniselt 4, korrutatakse arv 0,214 järjestikku 2-ga. Kui korrutamise tulemuseks on arv, mille täisarvuline osa on nullist erinev, siis kirjutatakse täisarvu osa eraldi (arvust vasakule). ja arv kirjutatakse täisarvu nullosaga. Kui korrutamise tulemuseks on null täisarvu osaga arv, siis kirjutatakse sellest vasakule null. Korrutamisprotsess jätkub, kuni murdosa jõuab puhta nullini või saame vajaliku arvu numbreid. Kirjutades ülevalt alla rasvaseid numbreid (joonis 4), saame kahendarvusüsteemis vajaliku arvu: 0. 0011011 .
Seetõttu võime kirjutada:
0.214 10 =0.0011011 2 .
Näide 8 . Teisendame arvu 0,125 kümnendarvusüsteemist kahendarvuks SS.
| 0.125 | ||
| x | 2 | |
| 0 | 0.25 | |
| x | 2 | |
| 0 | 0.5 | |
| x | 2 | |
| 1 | 0.0 |
Arvu 0,125 teisendamiseks kümnend-SS-st kahendarvuks korrutatakse see arv järjestikku 2-ga. Kolmandas etapis on tulemuseks 0. Järelikult saadakse järgmine tulemus:
0.125 10 =0.001 2 .
Näide 9 . Teisendame arvu 0,214 kümnendarvusüsteemist kuueteistkümnendsüsteemi SS-ks.
| 0.214 | ||
| x | 16 | |
| 3 | 0.424 | |
| x | 16 | |
| 6 | 0.784 | |
| x | 16 | |
| 12 | 0.544 | |
| x | 16 | |
| 8 | 0.704 | |
| x | 16 | |
| 11 | 0.264 | |
| x | 16 | |
| 4 | 0.224 |
Järgides näiteid 4 ja 5, saame numbrid 3, 6, 12, 8, 11, 4. Kuueteistkümnendsüsteemis vastavad numbrid 12 ja 11 aga numbritele C ja B. Seega on meil:
0,214 10 =0,36C8B4 16 .
Näide 10 . Teisendame arvu 0,512 kümnendarvusüsteemist kaheksandarvuks SS.
| 0.512 | ||
| x | 8 | |
| 4 | 0.096 | |
| x | 8 | |
| 0 | 0.768 | |
| x | 8 | |
| 6 | 0.144 | |
| x | 8 | |
| 1 | 0.152 | |
| x | 8 | |
| 1 | 0.216 | |
| x | 8 | |
| 1 | 0.728 |
Sain:
0.512 10 =0.406111 8 .
Näide 11 . Teisendame arvu 159.125 kümnendarvusüsteemist kahendarvuks SS. Selleks tõlgime eraldi arvu täisarvu (näide 4) ja arvu murdosa (näide 8). Neid tulemusi täiendavalt kombineerides saame:
159.125 10 =10011111.001 2 .
Näide 12 . Teisendame arvu 19673.214 kümnendarvusüsteemist kuueteistkümnendsüsteemi SS-ks. Selleks tõlgime eraldi arvu täisarvulise osa (näide 6) ja arvu murdosa (näide 9). Lisaks saame neid tulemusi kombineerides.