Algajatele

Mis on murdosa võrdsed osad. Murdarvu mõiste. Universaalsed õppetegevused

Olgu nõutav lõigu x pikkuse mõõtmine ühe lõigu e abil (joonis 27). Mõõtmisel selgus, et lõik x koosneb kolmest lõigust, mis on võrdne e-ga, ja lõigust, mis on lõigust e lühem. Sel juhul ei saa lõigu x pikkust väljendada naturaalarvuna.

Kui aga lõik e on jagatud 4 võrdseks osaks, koosneb lõik x 14 lõigust, mis on võrdne lõigu e neljanda osaga. Ja siis, rääkides lõigu x pikkusest, peame märkima kaks numbrit 4 ja 14: lõigu e neljas osa mahub lõigusse täpselt 14 korda. Seetõttu leppisime kokku, et kirjutame lõigu x pikkuse kui , kus E on ühiklõigu e pikkus ja nimetame sümbolit murdarvuks.

AT üldine vaade Murru mõiste defineeritakse järgmiselt.

Olgu antud segmentxja üks segmente, mille pikkusE. Kui segmentx
sisaldabmsegmendid, mis on võrdsedn-segmendi osae, seejärel lõigu pikkusxsaab esitada kui , kus sümbolit nimetatakse murdarvuks (ja loe "em nh").

Arvu murdosa kirjes m ja n- loomulik, m helistas lugeja , n – nimetaja fraktsioonid.

Murdu nimetatakse õigeks, kui selle lugeja on nimetajast väiksem, ja ebaõigeks, kui selle lugeja on nimetajast suurem või sellega võrdne.

Eelnevalt näidati, et lõigu e neljas osa sobib segmenti x täpselt 14 korda. Ilmselgelt pole see ainus võimalus segmendi sellise osa valimiseks e, mis sobib segmenti x täisarv kordi. Võite võtta kaheksandiku lõigust e, seejärel segment x koosneb 28 sellisest osast ja selle pikkust väljendatakse murdarvuna. Võite võtta lõigu kuueteistkümnenda osa
e, seejärel segment x koosneb 56 sellisest osast ja selle pikkust väljendatakse murdarvuna.

Üldjuhul saab sama lõigu x pikkust antud ühikulise segmendi e korral väljendada kui mitmesugused fraktsioonid, pealegi, kui pikkust väljendatakse murdena , siis saab seda väljendada ka vormi mis tahes murruna, kus k
– naturaalarv.

Teoreem. Murdude saamiseks ja sama lõigu pikkuse väljendamiseks on vajalik ja piisav, et võrdus on täidetud.

Jätame selle teoreemi tõestuse välja.

Kaks murdosa ja öeldakse olevat võrdsed, kui .

Kui murrud on võrdsed, siis kirjuta .

Näiteks kuna , a , kuna , a ja .

Eelpool sõnastatud teoreemidest ja definitsioonidest järeldub, et kaks murru on võrdsed siis ja ainult siis, kui nad väljendavad sama lõigu pikkust.

Teame, et murdude võrdsuse seos on refleksiivne, sümmeetriline ja transitiivne, s.t. on ekvivalentsuhe.

Võrdsete murdude määratlusest tuleneb murdosa põhiomadus. Tuletame talle meelde.

Kui murdosa lugeja ja nimetaja korrutada või jagatud sama arvuga, saad murru, mis on võrdne antud arvuga.

See omadus põhineb fraktsioonide vähendamisel ja fraktsioonide vähendamisel ühine nimetaja.

Fraktsiooni vähendamine - see on antud murru asendamine teisega, mis on võrdne antud murruga, kuid väiksema lugeja ja nimetajaga.

Kui murdu lugeja ja nimetaja jagavad mõlemad ainult ühega, siis nimetatakse seda murdu taandamatu. Näiteks - taandamatu murd, kuna selle lugeja ja nimetaja jagatakse samaaegselt ainult ühega, st D (5, 17) = 1.

Ühiku osa või mitut selle osa nimetatakse liht- või tavamurruks. Võrdsete osade arvu, milleks ühik on jagatud, nimetatakse nimetajaks ja võetud osade arvu lugejaks. Murd kirjutatakse järgmiselt:

AT sel juhul a on lugeja, b on nimetaja.

Kui lugeja on nimetajast väiksem, on murd väiksem kui 1 ja seda nimetatakse õige murdosa. Kui lugeja on nimetajast suurem, siis on murd suurem kui 1, siis nimetatakse murdu valeks murruks.

Kui murru lugeja ja nimetaja on võrdsed, siis on murd võrdne.

1. Kui lugeja saab jagada nimetajaga, siis see murd on võrdne jagamise jagatisega:

Kui jagamine toimub jäägiga, võib seda valet murdu esitada segaarvuga, näiteks:

Siis 9 on mittetäielik jagatis ( terve osa seganumber)
1 - jääk (murdosa lugeja),
5 on nimetaja.

Segaarvu teisendamiseks murdarvuks korrutage segaarvu täisarv nimetajaga ja lisage murdosa lugeja.

Saadud tulemus on hariliku murru lugeja ja nimetaja jääb samaks.

Tegevused murdarvudega

Fraktsiooni laiendamine. Murru väärtus ei muutu, kui selle lugeja ja nimetaja korrutada sama nullist erineva arvuga.
Näiteks:

Fraktsiooni vähendamine. Murru väärtus ei muutu, kui selle lugeja ja nimetaja jagada sama nullist erineva arvuga.
Näiteks:

Murdarvude võrdlus. Kahest fraktsioonist samad lugejad suurem, mille nimetaja on väiksem:

Kahest fraktsioonist samad nimetajad suurem, mille lugeja on suurem:

Erinevate lugejate ja nimetajatega murdude võrdlemiseks on vaja neid laiendada, st viia ühise nimetajani. Mõelge näiteks järgmistele murdudele:

Murdude liitmine ja lahutamine. Kui murdude nimetajad on samad, siis murdude liitmiseks on vaja liita nende lugejad ja murdude lahutamiseks nende lugejad. Saadud summa või erinevus on tulemuse lugeja, samas kui nimetaja jääb samaks. Kui murdude nimetajad on erinevad, tuleb esmalt murded taandada ühisele nimetajale. Segaarvude liitmisel liidetakse nende täis- ja murdosa eraldi. Segaarvude lahutamisel tuleb need esmalt vormile teisendada ebaõiged murded, siis lahutage üksteisest ja pärast seda viige tulemus vajaduse korral uuesti segaarvu kujule.

Murdude korrutamine. Murdude korrutamiseks peate korrutama nende lugejad ja nimetajad eraldi ning jagama esimese korrutise teisega.

Murdude jagamine. Arvu jagamiseks murdosaga peate selle arvu korrutama selle pöördarvuga.

Kümnend on ühe kümne, saja, tuhande jne jagamise tulemus. osad. Kõigepealt kirjutatakse numbri täisarvuline osa, seejärel asetatakse koma paremale. Esimene number pärast koma tähendab kümnendite arvu, teine - sajandikute arvu, kolmas - tuhandikute arvu jne. Koma järel olevaid numbreid nimetatakse kümnendkohtadeks.

Näiteks:

Kümnendarvu omadused

Omadused:

Kümnendmurd ei muutu, kui paremale lisada nullid: 4,5 = 4,5000.
Kümnendmurd ei muutu, kui eemaldada kümnendmurru lõpus asuvad nullid: 0,0560000 = 0,056.
Kümnendkoht suureneb 10, 100, 1000 jne juures. korda, kui liigutate koma ühele, kahele, kolmele jne. positsioonid paremale: 4,5 45 (murd on suurenenud 10 korda).
Kümnendkohta vähendatakse 10, 100, 1000 jne võrra. korda, kui liigutate koma ühele, kahele, kolmele jne. positsioonid vasakule: 4,5 0,45 (murd on vähenenud 10 korda).

Perioodiline kümnendkoht sisaldab lõputult korduvat numbrite rühma, mida nimetatakse perioodiks: 0,321321321321…=0, (321)

Tehted kümnendkohtadega

Kümnendkohtade liitmine ja lahutamine käib samamoodi nagu täisarvude liitmine ja lahutamine, tuleb vaid vastavad kümnendkohad üksteise alla kirjutada.
Näiteks:

Kümnendmurdude korrutamine toimub mitmes etapis:

Me korrutame kümnendkohad täisarvudena, võtmata arvesse koma.
Kehtib reegel: komakohtade arv korrutis võrdub kõigi tegurite kümnendkohtade summaga.

Näiteks:

Komakohtade arvude summa tegurites on: 2+1=3. Nüüd peate saadud numbri lõpust lugema 3 numbrit ja panema koma: 0,675.

Kümnendkohtade jagamine. Kümnendarvu jagamine täisarvuga: kui dividend on jagajast väiksem, tuleb jagatise täisarvu osasse kirjutada null ja selle järele panna koma. Seejärel lisage dividendi koma arvesse võtmata murdosa järgmine number selle täisarvule ja võrrelge saadud dividendi täisarvu uuesti jagajaga. Kui uus arv on jälle jagajast väiksem, tuleb toimingut korrata. Seda protsessi korratakse, kuni saadud dividend on suurem kui jagaja. Pärast seda tehakse jagamine nagu täisarvude puhul. Kui dividend on suurem või võrdne jagajaga, jagame kõigepealt selle täisarvu, kirjutame jagamise tulemuse jagatisesse ja paneme koma. Pärast seda jätkub jagamine, nagu täisarvude puhul.

Ühe kümnendmurru jagamine teiseks: esiteks kantakse koma koma dividendis ja jagajas jagajas olevate kümnendkohtade arvu järgi ehk teeme jagajast täisarvu ja sooritatakse ülalkirjeldatud toimingud.

Selleks, et pöörata kümnend tavaliseks, tuleb lugejaks võtta kümnendkoha järel olev arv ja nimetajaks kümnendarvu k-s aste (k on kümnendkohtade arv). Nullist erinev täisarvu osa jääb harilikus murrus alles; null täisarvu osa jäetakse välja.
Näiteks:

Hariliku murru kümnendkohaks teisendamiseks on vaja vastavalt jagamisreeglitele jagada lugeja nimetajaga.

Protsent on näiteks sajandik ühikust: 5% tähendab 0,05. Suhe on ühe arvu jagamise jagatis teisega. Proportsioon on kahe suhte võrdsus.

Näiteks:

Proportsiooni põhiomadus: proportsiooni äärmiste liikmete korrutis on võrdne selle keskmiste liikmete korrutisega, see tähendab 5x30 = 6x25. Kahte teineteisest sõltuvat suurust nimetatakse proportsionaalseks, kui nende suuruste suhe jääb muutumatuks (proportsionaalsuskoefitsient).

Seega selgub järgmised aritmeetilised tehted.
Näiteks:

Ratsionaalarvude hulk sisaldab positiivseid ja negatiivseid arve (täis- ja murdarvu) ning nulli. Matemaatikas aktsepteeritud ratsionaalarvude täpsem definitsioon on järgmine: arvu nimetatakse ratsionaalseks, kui seda saab esitada tavalise taandamatu murdena kujul:, kus a ja b on täisarvud.

Negatiivse arvu korral on absoluutväärtus (moodul) positiivne arv, mis saadakse selle märgi muutmisel "-" asemel "+"; positiivse arvu ja nulli korral arv ise. Arvu mooduli tähistamiseks kasutatakse kahte sirget, mille sisse see arv kirjutatakse, näiteks: |–5|=5.

Absoluutväärtuse omadused

Olgu antud arvu moodul , mille atribuudid kehtivad:

Monoom on kahe või enama teguri korrutis, millest igaüks on kas arv või täht või tähe aste: 3 x a x b. Koefitsienti nimetatakse enamasti ainult arvuliseks teguriks. Monoomide nimetatakse sarnasteks, kui need on samad või erinevad ainult koefitsientide poolest. Monoomi aste on kõigi selle tähtede eksponentide summa. Kui monomialide summa hulgas on sarnaseid, siis saab summat vähendada rohkemaks selge nägemine: 3 x a x b + 6 x a \u003d 3 x a x (b + 2). Seda toimingut nimetatakse sarnaste terminite või sulgude sundimiseks.

Polünoom on monomialide algebraline summa. Polünoomi aste on antud polünoomi kaasatud monomialide astmetest suurim.

Olemas järgmised valemid lühendatud korrutis:

Faktoreerimismeetodid:

Algebraline murd on vormi avaldis, kus A ja B võivad olla arv, monoom, polünoom.

Kui kaks avaldist (numbriline ja tähestikuline) on ühendatud märgiga "=", siis öeldakse, et need moodustavad võrdsuse. Igasugust tõelist võrdsust, mis kehtib kõigi selles sisalduvate tähtede lubatud arvväärtuste kohta, nimetatakse identiteediks.

Võrrand on sõnasõnaline võrdsus, mis kehtib selles sisalduvate tähtede teatud väärtuste korral. Neid tähti nimetatakse tundmatuteks (muutujateks) ja nende väärtusi, mille juures antud võrrand muutub identiteediks, nimetatakse võrrandi juurteks.

Võrrandi lahendamine tähendab kõigi selle juurte leidmist. Kaht või enamat võrrandit peetakse samaväärseks, kui neil on samad juured.

null oli võrrandi juur;
Võrrandil on ainult piiratud arv juuri.

Algebraliste võrrandite peamised tüübid:

Lineaarvõrrandis on ax + b = 0:

kui a x 0, on üks juur x = -b/a;
kui a = 0, b ≠ 0, siis pole juuri;
kui a = 0, b = 0, on juur suvaline reaalarv.

Võrrand xn = a, n N:

kui n - paaritu number, mille reaaljuur on võrdne a/n-ga iga a korral;
kui n on paarisarv, siis 0 korral on sellel kaks juurt.

Põhilised identsed teisendused: ühe avaldise asendamine teisega, sellega identselt võrdne; võrrandiliikmete ülekandmine ühelt küljelt teisele vastandmärkidega; võrrandi mõlema osa korrutamine või jagamine sama avaldise (arvuga), mis ei ole null.

Lineaarvõrrand ühe tundmatuga on võrrand kujul: ax+b=0, kus a ja b on teadaolevad numbrid, ja x on tundmatu suurus.

Kahe tundmatuga lineaarvõrrandi süsteemid on järgmise kujuga:

Kus a, b, c, d, e, f on antud numbrid; x, y on teadmata.

Arvud a, b, c, d - tundmatute koefitsiendid; e, f - vabaliikmed. Selle võrrandisüsteemi lahenduse saab leida kahe põhimeetodi abil: asendusmeetod: ühest võrrandist väljendame ühe tundmatu läbi koefitsientide ja teise tundmatu ning seejärel asendame selle teise võrrandiga, lahendades viimase võrrandi. , leiame esmalt ühe tundmatu, seejärel asendame leitud väärtuse esimese võrrandiga ja leiame teise tundmatu; meetod ühe võrrandi liitmiseks või teisest lahutamiseks.

Operatsioonid juurtega:

Aritmeetika n-nda juur kraadi mittenegatiivsest arvust a nimetatakse mittenegatiivseks arvuks, n aste mis on võrdne a. algebraline juur n aste antud arvust kutsutakse välja kõigi selle arvu juurte hulk.

Irratsionaalarvusid, erinevalt ratsionaalsetest, ei saa esitada tavalise taandamatu murdona kujul m/n, kus m ja n on täisarvud. Need on uut tüüpi arvud, mida saab arvutada mis tahes täpsusega, kuid mida ei saa asendada ratsionaalarvuga. Need võivad ilmneda geomeetriliste mõõtmiste tulemusena, näiteks: ruudu diagonaali pikkuse ja selle külje pikkuse suhe on võrdne.

Ruutvõrrand on teise astme algebraline võrrand ax2+bx+c=0, kus a, b, c on antud numbrilised või tähestikulised koefitsiendid, x on tundmatu. Kui jagada kõik selle võrrandi liikmed a-ga, saame tulemuseks x2+px+q=0 - taandatud võrrandi p=b/a, q=c/a. Selle juured leitakse järgmise valemiga:

Kui b2-4ac>0, siis on kaks erinevat juurt, b2-4ac=0, siis on kaks võrdset juurt; b2-4ac Mooduleid sisaldavad võrrandid

Peamised mooduleid sisaldavad võrrandite tüübid:
1) |f(x)| = |g(x)|;
2) |f(x)| = g(x);
3) f1(x)|g1(x)| + f2(x)|g2(x)| + … + fn(x)|gn(x)| =0, n N, kus f(x), g(x), fk(x), gk(x) on antud funktsioonid.

Detailselt lahti võetud murdosa põhiomadus, on toodud selle sõnastus, toodud tõestus ja selgitav näide. Vaadeldakse ka murdu põhiomaduse rakendamist murdude vähendamisel ja murdude taandamisel uuele nimetajale.

Leheküljel navigeerimine.

Murru põhiomadus - sõnastus, tõestus ja selgitavad näited

Kõik harilikud murded on üks väga oluline vara, mida nimetatakse murdosa põhiomaduseks. Sõnastame murdosa põhiomadus: kui murdu lugeja ja nimetaja korrutada või jagada sama naturaalarvuga, siis saadakse antud murdarvuga võrdne murd.

Kirjutame murdu põhiomaduse sõnasõnalisel kujul: naturaalarvude a, b ja m korral kehtivad võrrandid ja.

Toome murru põhiomaduse tõend. Võrdused (a m) b=(b m) a ja (a: m) b=(b: m) a kehtivad naturaalarvude korrutamise ja naturaalarvude jagamise omaduste tõttu, siis murrud ja , ja on ka definitsiooni järgi võrdsed (vt võrdsed ja ebavõrdsed murrud).

Vaatame näidet, mis illustreerib murdosa põhiomadust. Oletame, et meil on ruut, mis on jagatud 9 "suureks" ruuduks ja kõik need "suured" ruudud on jagatud 4 "väikseks" ruuduks. Seega võime ka öelda, et algne ruut on jagatud 4·9=36 "väikese" ruuduga. Värvime üle 5 "suurt" ruutu. Sel juhul täidetakse 4 5 = 20 “väikest” ruutu. Esitame meie näitele vastava joonise.

Varjutatud osa on 5/9 algsest ruudust või, mis on sama, 20/36 algsest ruudust, see tähendab, et murrud 5/9 ja 20/36 on võrdsed: või . Nendest võrdustest, aga ka võrdustest 20=5 4, 36=9 4, 20:4=5 ja 36:4=9 järeldub, et ja .

Lahtivõetud materjali konsolideerimiseks kaaluge näite lahendust.

Mõne hariliku murru lugeja ja nimetaja korrutati 62-ga, mille järel saadud murru lugeja ja nimetaja jagati 2-ga. Kas saadud murd on võrdne originaaliga?

Murru lugeja ja nimetaja korrutamine suvalise naturaalarvuga, eriti 62-ga, annab murdosa, mis murru põhiomaduse tõttu on võrdne esialgsega. Murru põhiomadus võimaldab meil ka väita, et pärast saadud murru lugeja ja nimetaja jagamist 2-ga saadakse murd, mis võrdub algse murruga.

Jah, saadud murd on võrdne originaaliga.

Murru põhiomaduse rakendamine

Murru põhiomadust rakendatakse peamiselt kahel juhul: esiteks murdude taandamisel uuele nimetajale ja teiseks murdude vähendamisel.

Murru taandamine uuele nimetajale on algse murru asendamine sellega võrdse, kuid suurema lugeja ja nimetajaga. Murru viimiseks uude nimetajasse korrutatakse nii murru lugeja kui ka nimetaja mingi naturaalarvuga ja vastavalt murdosa põhiomadusele saadakse murd, mis on võrdne algse arvuga, kuid erinev lugeja ja nimetaja. Tavaliste murdudega tehteid tehes ei saa te hakkama ilma murdude taandamata uue nimetajani.

Murru põhiomadus võimaldab teil murde vähendada ja selle tulemusel liikuda algsest murrust sellega võrdsele murdarvule, kuid väiksema lugeja ja nimetajaga. Murru taandamine seisneb algmurru lugeja ja nimetaja jagamises lugeja ja nimetaja mis tahes positiivse ühisjagajaga peale ühe (kui selliseid ühiseid jagajaid pole, siis on algmurd taandamatu, st seda ei saa taandada ). Eelkõige toob suurima ühisjagajaga jagamine algse murdosa taandamatusse vormi.

www.cleverstudents.ru

Murru põhiomadus

Harilike murdude võrdlemiseks, liitmiseks või lahutamiseks erinevad nimetajad, tuleb need esmalt viia sama (ühe) nimetajani.

Selleks jagatakse arv, millest osa võetakse osadeks (arvu osakute arv määrab nimetaja), jagatakse suuremaks arvuks osadeks nii, et kõik murdude nimetajad on üksteise kordsed.

Näiteks tuleb võrrelda, liita või lahutada murde ja. Vaatleme joonisel jaotust aktsiateks (1 jagati 4 osaks ja 1 jagunes 2 osaks), 1 võetakse tervikuna.

Jagades 2 aktsiaga, saame visuaalse võrdluse.

See tähendab, et kuna aktsiad sisaldavad 2 aktsiat, kirjutame: . Vastavalt aritmeetika reeglitele: Valime lugejas ja nimetajas algtegurid:

Ülaltoodud joonised võimaldavad tuletada reegli nimega murdosa põhiomadus.

Reegel. Murru lugeja ja nimetaja saab korrutada või jagada sama naturaalarvuga, millest murru väärtus ei muutu.

Kui uue murru lugejat esindab esimese murru ja mis tahes naturaalarvu korrutis (või jagatis) ning uue murru nimetaja on esimese murru ja sama arvu nimetaja korrutis (või jagatis) , siis säilitab uus murru väärtuse (väärtuse) korrutiste (või jagandite) arvutamisel algse murru, nii et saate antud ja saadud murdude vahele panna võrdusmärgi.

Võib kirjutada murdosa põhiomadus murdosa lugeja ja nimetaja korrutamisel arvuga:

Võib kirjutada murdosa põhiomadus murdosa lugeja ja nimetaja jagamisel arvuga:

Fraktsiooni vähendamine

Murdude abil saab terve objekti sama osa kirjutada erineval viisil.

Pool ringist on joonisel varjutatud

Seega on kõik need murrud võrdsed.

Murd

Mugavuse huvides kirjutatakse murru kohale paremale jäävale kaldkriipsule lisategur.

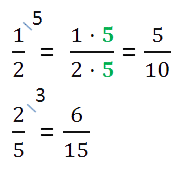
Läheme tagasi oma murdude juurde ja kirjutame need teises järjekorras.

Antud ühega võrdse murdosa saab, kui murdosa lugeja ja nimetaja jagatakse samaaegselt sama arvuga, mis ei ole võrdne nulliga.

Seda murru teisendust nimetatakse fraktsiooni vähendamine.

Murru taandamine kirjutatakse tavaliselt järgmiselt.

Lugeja ja nimetaja kriipsutatakse maha ning nende kõrvale kirjutatakse sama arvuga lugeja ja nimetaja jagamise (jagatised) tulemused.

Arv, millega lugeja ja nimetaja jagati, peetakse silmas.

Meie näites vähendasime (st jagasime nii lugeja kui ka nimetaja) murdosa kahega, mida pidasime meeles.

Fraktsiooni vähendamist saab läbi viia järjestikku.

Sõnastame murdosa põhiomaduse.

Kui murdosa lugeja ja nimetaja korrutada või jagada sama arvuga, mis ei ole võrdne nulliga, saadakse antud murdarvuga võrdne murd.

Kirjutame selle omaduse sõnasõnaliste väljendite kujul.

, kus "a", "b" ja "k" on naturaalarvud.

Murru põhiomadus. Fraktsiooni vähendamine. Murdude võrdsus.

Murdude võrdsus.

See teema on üsna oluline murdude põhiomaduste osas, kogu edasine matemaatika ja algebra põhinevad. Murdude vaadeldavad omadused on hoolimata nende tähtsusest väga lihtsad.

Aru saama murdude põhiomadused kaaluge ringi.

Ringil on näha, et 4 osa või jagamist on varjutatud kaheksast võimalikust. Kirjutage üles saadud murd \(\frac \)

Järgmine ring näitab, et üks kahest võimalikust osast on varjutatud. Kirjutage saadud murd \(\frac \)

Kui me vaatame lähemalt, näeme, et esimesel juhul, et teisel juhul on pool ringist varjutatud, nii et saadud murrud on võrdsed \(\frac = \frac \), see tähendab, et see on sama number.

Kuidas seda matemaatiliselt tõestada? Väga lihtsalt pidage meeles korrutustabelit ja kirjutage esimene murdosa teguriteks.

Mida me oleme teinud? Värvisime lugeja ja nimetaja teguriteks \(\frac > >\) ning seejärel jagasime murrud \(\frac \cdot \color \). Neli jagatud neljaga on 1 ja üks korrutatuna mis tahes arvuga on arv ise. Seda, mida oleme ülaltoodud näites teinud, nimetatakse fraktsioonide vähendamine.

Vaatame teist näidet ja vähendame murdosa.

Värvisime lugeja ja nimetaja uuesti teguriteks ning taandasime samad arvud lugejateks ja nimetajateks. See tähendab, et kaks jagatuna kahega annab ühe ja üks korrutatuna mis tahes arvuga annab sama arvu.

Murru põhiomadus.

See tähendab murdosa peamist omadust:

Kui nii murdosa lugeja kui ka nimetaja korrutada sama arvuga (v.a null), siis murru väärtus ei muutu.

Lugeja ja nimetaja saate samal ajal jagada ka sama arvuga.
Kaaluge näidet:

Kui murdu nii lugeja kui ka nimetaja jagada sama arvuga (v.a null), siis murru väärtus ei muutu.

Nimetatakse murde, millel on ühised algjagajad nii lugejates kui ka nimetajates tühistatavad murded.

Vähendatud murru näide: \(\frac , \frac , \frac , \frac , …\)

On olemas ka taandamatuid murde.

taandamatu murdosa on murd, millel ei ole lugejates ja nimetajates ühiseid algjagajaid.

Näide taandamatust murdosast: \(\frac , \frac , \frac , \frac , …\)

Mis tahes arvu saab esitada murruna, sest iga arv jagub ühega, näiteks:

Küsimused teema kohta:
Kas arvate, et mõnda murdosa saab vähendada või mitte?
Vastus: Ei, on taandatavad murrud ja taandamatud murded.

Kontrollige, kas võrdus on tõene: \(\frac = \frac \)?
Vastus: kirjuta murdosa \(\frac = \frac = \frac \) jah aus.

Näide nr 1:
a) Leidke murd, mille nimetaja on 15, võrdne murdosaga \(\frac\).
b) Leidke murdarvuga võrdne murd, mille lugeja on 8 \(\frac\).

Lahendus:
a) Nimetajaks peab olema arv 15. Nüüd on nimetajaks arv 3. Millise arvuga tuleks arv 3 korrutada, et saada 15? Tuletame meelde korrutustabelit 3⋅5. Peame kasutama murdude põhiomadust ja korrutama nii murdarvu lugeja kui ka nimetaja \(\frac\) poolt 5.

b) Lugejas on vaja numbrit 8. Nüüd on lugejas arv 1. Millise arvuga tuleks arv 1 korrutada, et saada 8? Muidugi 1⋅8. Peame kasutama murdude põhiomadust ja korrutama nii murdarvu lugeja kui ka nimetaja \(\frac\) 8. Saame:

Näide nr 2:
Leidke murdosaga võrdne taandamatu murd: a) \(\frac\), b) \(\frac\).

Näide nr 3:
Kirjutage arv murruna: a) 13 b) 123

Tund murdude võrdsuse teemal, klass 5, õpik Nikolsky S. M. jt.

Kasutage Infouroki kursustelt kuni 50% allahindlust

Tuletame meelde, et vastavalt õpetaja kutsestandardile (kinnitatud Venemaa Tööministeeriumi korraldusega), kui teil ei ole õpetatavale ainele vastavat haridust, siis Peate läbima erialase ümberõppe pedagoogilise tegevuse valdkonnas. Seda saad teha kaugjuhtimisega projekti "Infourok" kodulehel ja saada kvalifikatsiooniga diplom 2 kuuga!

Töötab ainult praegu 50% SOODSAMALT kõigile õpetajatele kõigile 111 erialasele ümberõppe kursusele! Järelmaksu saab vaid 10% sissemaksega, samas kursuse hind järelmaksu kasutamise tõttu ei tõuse!

Praktilise töö kaart.docx

Kaart 1

2. kaart

Harjutus. Vaadake pilte ja tehke järeldus murrude võrdsuse kohta.

Vihje 1. Kui palju ringe ja ruute on varjutatud?

Vihje 1. Kirjutage üles murrud, mis tähistavad iga kujundi varjutatud osa.

Vihje 2. Tee järeldus saadud murdude võrdsuse kohta.

Vaatamiseks valitud dokument Marsruutimine matemaatika tund 5. klassis.docx

5. klassi matemaatikatunni tehnoloogiline kaart

Tunni teema: "Murdude võrdsus" (õpik "Matemaatika 5", Nikolsky S. M., Potapov M. K. jt)

Tunni eesmärgid (ülesanded):

— tutvustada õpilastele murdu põhiomadust, näidata selle rakendust murdude vähendamisel;

- õppida taandama murde ja määrama taandamatut;

— arendada oskust rakendada matemaatilisi teadmisi praktiliste probleemide lahendamisel;

- arendada käitumiskultuuri rühmatööd;

- arendada huvi aine vastu.

- teadma murru põhiomadust, murdude redutseerimise ja taandamatute murdude definitsiooni;

- oskama tuua murde uude nimetajasse, vähendada murde;

mõista ülesande tähendust; algatusvõime, leidlikkus, aktiivsus matemaatikaülesannete lahendamisel;

- nägemisvõime matemaatika ülesanne probleemse olukorra kontekstis;

- algoritmide ettekirjutuste olemuse mõistmine ja oskus tegutseda vastavalt pakutud algoritmile.

Tunni tüüp, pedagoogiline tehnoloogia

Uue, problemaatilise dialoogitehnoloogia õppimine.

Tahvel, kriit, arvuti multimeediaprojektoriga, interaktiivne tahvel, jaotusmaterjalid, kehalise kasvatuse video, enesehindamislehed

Põhimõisted, terminid

Uued mõisted ja nendevahelised seosed

Redutseeritav murd, taandamatu murd

Kontroll, enesekontroll klassiruumis

Kasutatud meetodid, tehnikad, vormid

Universaalsed õppetegevused

I. Aja organiseerimine.

Alates sellest ajast saite märkmikud kätte vaheajal kodutöö Kõik sai tehtud ja probleeme polnud.

Näitab lahke tähelepanu.

Õppevahendite olemasolu kontrollimine, ratsionaalne paigutamine lauale

Vastastikune tervitamine, kohalolijate kontroll, klassiruumi tunniks valmisoleku kontrollimine.

Õpilaste valmisolek õppimiseks, tegevusteks

II. Teadmiste värskendus

Tuletagem meelde, mida me eelmistes tundides õppisime. Mida me uurisime? (murrud)

1. Mis on kirjutatud murru rea alla?

2.Mida see näitab?

3. Mis on kirjutatud murru rea kohale?

4.Mida see näitab?

5. Millise toiminguga asendatakse murdosa kriips?

6. Leidke ¼ 120-st.

(mitmeks osaks on tervik jagatud)

(mitu osa neist võtsite)

Testülesanded, vastused antakse erinevat värvi signaalide abil

Regulatiivne: tahtlik eneseregulatsioon.

Isiklik : tähenduse kujunemise tegevus, õppimise motivatsioon

hariduskoostöö planeerimine õpetaja ja kaaslastega.

Uueks avamiseks valmis

III . Probleemi sõnastamine

Nüüd teen teile ettepaneku lahendada selline probleem-muinasjutt. probleemne ülesanne

Teatud kuningriigis, teatud osariigis ta elas - seal oli kuningas ja tal oli kolm poega. Kuidagi kutsus ta pojad kokku ja ütles: “Te olete mu kallid pojad, tundub, et mul on aeg pensionile minna. Ma kogusin teid, et jagada teie vahel pärand, meie kuningriik on riik. Jah, selles on häda – meie teadlased on justkui midagi sassi ajanud. Sulle, mu vanim poeg, on meie osariik maha kantud, sulle, mu keskmine poeg, ja sulle, mu noorim. Noorim poeg oli nördinud: "Miks mind petti?" Ja vennad tülitsesid omavahel. Ja kuningas andis välja määruse: „Kellel õnnestub viga leida ja mu pojad lepitada, ootab teda kuninglik tasu. ”

Poisid, kas me saame kuninga ja tema pojad lepitada? Mida me peame selle jaoks välja selgitama?

Mida me siis tõenäoliselt tänases tunnis õpime?

Ja proovime sõnastada oma tunni teema.

Avage vihikud, kirjutage neisse tunni "Murdude võrdsus" number, klassitöö ja teema.

(Kas murrud on võrdsed või mitte)

(Saate teada, kas murrud on võrdsed või mitte)

tunni eesmärgi sõnastamine

Probleemi püstitus, eesmärgi sõnastamine, tunni teemad

IV. Õpiprobleemi lahendamise planeerimine

Aidake mul nüüd õppetundi planeerida, st määrata, mida me teeme.

(1. Õppige kindlaks tegema, kas murrud on võrdsed või mitte.

Regulatiivne: kognitiivse tegevuse planeerimine

Tunniplaani koostamine

Vana Hiina vanasõna ütleb: "Ma kuulen ja unustan, ma näen ja mäletan, ma teen ja saan aru." Ja selleks, et tänase tunni teemast aru saada, viime läbi praktilise töö.

Igaühel teist on laual kaardid.

Võtke kaart 1.

Töötame ruuduga. Jagage ruut neljaks võrdseks osaks ja värvige neist kolm. Mis osa

ruut osutus varjutatuks?

Jagage iga veerand ruudust 4 ossa. Mitu osa nüüd

Ja kui palju selliseid osi on väljaku kolmes varjutatud veerandis?

Milline ruudu osa on varjutatud?

Mida saate öelda murdude ¾ ja 12/16 kohta?

Võtke kaart 2 ja vastake küsimustele:

1. Millist osa tervikust on joonistel kujutatud ja üle maalitud? Kirjutage iga ringi alla, milline osa sellest on varjutatud.

Mida saate nende murdude kohta öelda?

See tähendab, et sama osa saab kirjutada erineval viisil.

Vaatame neid murde lähemalt. Kuidas saab ühest murrust teise murdosa, näiteks kuidas saab ¾-st 12/16?

Ja kuidas saada 4/8-st 2/4, ½?

Lõpetame, sõnastame reegli:

Poisid, äsja sõnastatud omadus on väga oluline ja seda nimetatakse murdosa peamiseks omaduseks.

Palun kirjutage reeglid ja valemid tahvlilt üles.

a, b, c on loomulikud. Pöörake sellele tähelepanu, see on väga oluline, sest te ei saa 0-ga jagada.

(korrutage lugeja ja nimetaja 4-ga)

(jagage lugeja ja nimetaja 2-ga, 4-ga)

(Murru lugeja ja nimetaja korrutamisel ja jagamisel sama arvuga (välja arvatud 0), siis selle väärtus ei muutu .)

Kognitiivne: võrdlus, üldistus, järelduse sõnastamine

Praktiliste tööde tegemine. Murru põhiomaduse formuleerimine

VI . Tegevusviisi kujundamine

Väljendage järgmised murrud: murduna nimetajaga 12.

Kujutage ette järgmisi murde: murduna nimetajaga 3.

Kirjutatud: asendada murded väiksemate nimetajatega võrdsed murrud. Poisid, seda transformatsiooni, mille me just sooritasime, nimetatakse fraktsioonide vähendamine.

Kirjutage ekraanilt üles, mis on murdosa vähendamine.

Jagage murdosa lugeja ja nimetaja sama arvuga lõika see maha.

Kui murdu lugejal ja nimetajal pole ühiseid algjagajaid, siis nimetatakse seda murdu. taandamatu.

Täitke ülesandeid. Kirjutage vihikusse, mis on murdude taandamine ja mis on taandamatu murd.

Regulatiivne: toimingute ja tulemuste korrigeerimine

Murru põhiomaduse esmane assimilatsioon ja rakendamine, murdude redutseerimise määratlused, taandamatu murd

VII . Uute teadmiste ja tegevusviiside kujundamine

Läheme nüüd tagasi oma tunniplaani juurde. Mida me juba teinud oleme? Mida on veel vaja teha?

Suurepärane. Nüüd soovitan teil natuke mängida.

Liigume kahte rühma. Kõigi pakutud murdude esimene rühm (I rida).

valib murrud, mis on võrdsed 1/2-ga, ja teine rühm (II rida) valib murrud, mis on võrdsed 1/3-ga.

Ja nüüd kontrollime, kuidas te ülesandega hakkama saite.

Nüüd pöördume tagasi vapustava probleemi juurde, mis meile tunni alguses raskusi valmistas. Ütle mulle, nüüd saad vastata probleemi küsimusele: kas kuninga nõuandjad ajasid midagi sassi?

Ja nüüd harjutame veel natuke. Võtke lehed oma kätesse treeningharjutused Lugege ülesanded hoolikalt läbi ja täitke need.

(Õppisime kindlaks tegema, kas murrud on võrdsed. Vaja on harjutada)

(Nüüd saame. Pärand jagati võrdselt, kuna esitatud murrud on võrdsed)

Treeningharjutused kaartidel

Töö interaktiivse tahvliga. Rühmatöö

Kommunikatiivne: rühmas osalejate eesmärkide ja funktsioonide kindlaksmääramine; algatuslik koostöö; partneri tegevuse kontrollimine, korrigeerimine, hindamine.

Uute teadmiste ja tegevusmeetodite rakendamine ja arendamine

VIII . Tunni kokkuvõtte tegemine, mõtisklus, kodutöö

See teema on üsna oluline murdude põhiomaduste osas, kogu edasine matemaatika ja algebra põhinevad. Murdude vaadeldavad omadused on hoolimata nende tähtsusest väga lihtsad.

Aru saama murdude põhiomadused kaaluge ringi.

Ringil on näha, et 4 osa või on varjutatud kaheksast võimalikust. Kirjutage saadud murd \(\frac(4)(8)\)

Järgmine ring näitab, et üks kahest võimalikust osast on varjutatud. Kirjutage saadud murd \(\frac(1)(2)\)

Kui me vaatame tähelepanelikult, näeme, et esimesel juhul, et teisel juhul on pool ringist varjutatud, seega on saadud murrud võrdsed \(\frac(4)(8) = \frac(1) (2)\), see tähendab, et see on sama number.

Kuidas seda matemaatiliselt tõestada? Väga lihtsalt pidage meeles korrutustabelit ja kirjutage esimene murdosa teguriteks.

\(\frac(4)(8) = \frac(1 \cdot \color(punane) (4))(2 \cdot \color(punane) (4)) = \frac(1)(2) \cdot \värv(punane) (\frac(4)(4)) =\frac(1)(2) \cdot \color(punane)(1) = \frac(1)(2)\)

Mida me oleme teinud? Võtsime arvesse lugeja ja nimetaja \(\frac(1 \cdot \color(red) (4))(2 \cdot \color(red) (4))\) ning seejärel jagasime murrud \(\frac(1) ) (2) \cdot \color(red) (\frac(4)(4))\). Neli jagatud neljaga on 1 ja üks korrutatuna mis tahes arvuga on arv ise. Seda, mida oleme ülaltoodud näites teinud, nimetatakse fraktsioonide vähendamine.

Vaatame teist näidet ja vähendame murdosa.

\(\frac(6)(10) = \frac(3 \cdot \color(punane) (2))(5 \cdot \color(punane) (2)) = \frac(3)(5) \cdot \värv(punane) (\frac(2)(2)) =\frac(3)(5) \cdot \color(punane)(1) = \frac(3)(5)\)

Murru põhiomadus.

See tähendab murdosa peamist omadust:

Kui nii murdosa lugeja kui ka nimetaja korrutada sama arvuga (v.a null), siis murru väärtus ei muutu.

\(\bf \frac(a)(b) = \frac(a \cdot n)(b \cdot n)\)

Lugeja ja nimetaja saate samal ajal jagada ka sama arvuga.
Kaaluge näidet:

\(\frac(6)(8) = \frac(6 \div \värv(punane) (2))(8 \div \värv(punane) (2)) = \frac(3)(4)\)

Kui murdu nii lugeja kui ka nimetaja jagada sama arvuga (v.a null), siis murru väärtus ei muutu.

\(\bf \frac(a)(b) = \frac(a \div n)(b \div n)\)

Nimetatakse murde, millel on ühised algjagajad nii lugejates kui ka nimetajates tühistatavad murded.

Tühistamise näide: \(\frac(2)(4), \frac(6)(10), \frac(9)(15), \frac(10)(5), …\)

On olemas ka taandamatuid murde.

taandamatu murdosa on murd, millel ei ole lugejates ja nimetajates ühiseid algjagajaid.

Redutseerimata murru näide: \(\frac(1)(2), \frac(3)(5), \frac(5)(7), \frac(13)(5), …\)

Mis tahes arvu saab esitada murruna, sest iga arv jagub ühega, näiteks:

\(7 = \frac(7)(1)\)

Küsimused teema kohta:
Kas arvate, et mõnda murdosa saab vähendada või mitte?
Vastus: Ei, on taandatavad murrud ja taandamatud murded.

Kontrollige, kas võrdus on tõene: \(\frac(7)(11) = \frac(14)(22)\)?
Vastus: kirjuta murdosa \(\frac(14)(22) = \frac(7 \cdot 2)(11 \cdot 2) = \frac(7)(11)\) jah aus.

Näide nr 1:
a) Leia murd, mille nimetaja on 15 ja mis on võrdne murruga \(\frac(2)(3)\).
b) Leidke murdarvuga võrdne murd, mille lugeja on 8 \(\frac(1)(5)\).

\(\frac(2)(3) = \frac(2 \cdot 5)(3 \cdot 5) = \frac(10)(15)\)

\(\frac(1)(5) = \frac(1 \cdot 8)(5 \cdot 8) = \frac(8)(40)\)

Näide nr 2:
Leidke murdosaga võrdne taandamatu murd: a) \(\frac(16)(36)\), b) \(\frac(10)(25)\).

Lahendus:
a) \(\frac(16)(36) = \frac(4 \cdot 4)(9 \cdot 4) = \frac(4)(9)\)

b) \(\frac(10)(25) = \frac(2 \cdot 5)(5 \cdot 5) = \frac(2)(5)\)

Näide nr 3:
Kirjutage arv murruna: a) 13 b) 123

Lahendus:
a) \(13 = \frac(13) (1)\)

b) \(123 = \frac(123) (1)\)

Tegevusi murdudega reguleerib murdosa põhiomadus: kui murdu lugeja ja nimetaja korrutada või jagada sama naturaalarvuga, siis saadakse sellega võrdne murd.

2/5 = 4/10, sest 2∙2/5∙2

Võrdsed murrud on sisuliselt sama arvu kirje.

Võrdle, 2/5 = 0,4 ja 4/10 = 0,4.

Nimetatakse numbreid, mida saame kirjutada murdudena ratsionaalsed arvud, mille hulk on tähistatud ladina tähega Q. Tuletame meelde, et iga täisarvu saame kirjutada murruna: 4 = 4/1, seega on iga täisarv ratsionaalne. Teisisõnu, täisarvude hulk Z on Q alamhulk või Z kuulub Q-sse.

Nii et korrutame murdosa 5-ga: 1/5 ∙ 5 = 1 ∙ 5/5 ∙ 5 = 5/25.

Jagage murdarvuga 3: 33/21: 3 = 33: 3/21: 3 = 11/7 = 14/7.

Murru lugeja ja nimetaja korrutamist sama arvuga nimetatakse nimetaja vähendamiseks.

Näiteks: kui korrutame murdarvu 3/4 2-ga ja saame 6/8, siis ütleme, et oleme taandanud murdosa 3/4 nimetajaks 8 ja arvu 2 nimetatakse lisateguriks.

Toome murdosa 4/5 nimetajasse 30.

1. Leidke lisategur: 30: 5 = 6. Seega on meie lisategur 6.

2. Korrutage murdosa lugeja ja nimetaja 6-ga: 4 ∙ 6/5 ∙ 6 = 24/30.

Niisiis, meie murdosa on 24/30.

Murru põhiomaduse põhjal jõuame mõisteni "fraktsiooni vähendamine". Murru taandamine on murdosa lugeja ja nimetaja jagamine nende ühise jagajaga (muu kui üks).

Võtke arvesse murdosa 15/20. Arvude 15 ja 20 arv 5 on ühine jagaja. See tähendab, et nii murdu lugeja kui ka nimetaja saab jagada murru 5 ühisjagajaga. Saame: 15: 5/20: 5 = 3/4.

Suurim ühisjagaja on suurim arv, mille võrra saab murdosa vähendada. Näiteks murdosa 30/45 saab vähendada 3 ja 5 võrra, kuid suurim arv, mille võrra saab meie murdosa vähendada, on arv 15: 30: 15 / 45: 15 = 2/3.

Juhtub, et murdu lugejal ja nimetajal pole ühtki ühist jagajat, välja arvatud üks; nimetame sellist murdu taandamatuks ja numbreid, millel pole peale ühe ühiseid jagajaid, nimetatakse kaasalgarvuks.

Murdude taandamine ühiseks nimetajaks võimaldab võrrelda erinevate nimetajatega murde. Teisisõnu, erinevate nimetajatega murdude võrdlemiseks peate:

1. tuua murrud ühisesse nimetajasse;
2. võrrelge saadud murdude lugejaid.

Vaatleme näidet 3/5 ??? 4/7.

1. Toome murrud ühise nimetajani 35. Selleks korruta esimene murd 7-ga (nii lugeja kui ka nimetaja) ja teine (nii lugeja kui nimetaja) 5-ga. Saame: 21/35 ? ?? 20/35.

2. Võrrelge saadud murdude lugejaid: 21 on suurem kui 20, seega 3/5 > 4/7.

Vaatleme näidet: 6/9 ??? 8/12.

Meie murdude ühiseks nimetajaks on arv 9 ∙ 12. Kuid näite lahendamise hõlbustamiseks tuleb märkida, et meie murde saab vähendada (6/9 3, 8/12 4): 2/ 3 ??? 2/3, s.o. 2/3 = 2/3, seega 6/9 = 8/12. Nagu näete, kulus meil antud juhul palju vähem aega murdude võrdsuse kindlakstegemiseks.