Для новаків

Що таке рівні частини дробу. Концепція дробу. Універсальні навчальні дії

Нехай потрібно виміряти довжину відрізка x за допомогою одиничного відрізка e (рис.27). При вимірі виявилося, що відрізок x складається з трьох відрізків, рівних e і відрізка, який коротше відрізка e. І тут довжина відрізка x може бути виражена натуральним числом.

Однак якщо відрізок e розбити на 4 рівні частини, то відрізок x виявиться, що складається з 14 відрізків, рівних четвертій частині відрізка e. І тоді, говорячи про довжину відрізка x, ми повинні вказати два числа 4 і 14: четверта частина відрізка e укладається у відрізку точно 14 разів. Тому умовилися довжину відрізка x записувати як , де E – довжина одиничного відрізка e, а символ називати дробом.

У загальному виглядіпоняття дробу визначають так.

Нехай дані відрізокxта одиничний відрізокe, довжина якогоE. Якщо відрізокx
складається зmвідрізків, рівнихn-ої частини відрізкаe, то довжина відрізкаxможе бути представлена у вигляді , де символ називають дробом (і читають "ем енних").

У записі дробу числа mі n- натуральні, mназивається чисельником , n – знаменником дроби.

Дроб називається правильним, якщо його чисельник менше знаменника, і неправильним, якщо його чисельник більший за знаменник або дорівнює йому.

Раніше показано, що четверта частина відрізка e уклалася у відрізку xточно 14 разів. Очевидно, це не єдиний варіант вибору такої частини відрізка e, що укладається у відрізок xціле число разів. Можна взяти восьму частину відрізка eтоді відрізок xскладатиметься з 28 таких частин і його довжина виражатиметься дробом. Можна взяти шістнадцяту частину відрізка
eтоді відрізок xскладатиметься з 56 таких частин і його довжина виражатиметься дробом.

Взагалі довжина того самого відрізка x при заданому одиничному відрізку e може виражатися різними дробами, причому, якщо довжина виражена дробом , то вона може бути виражена і будь-яким дробом виду , де k
– натуральне число.

Теорема.Для того щоб дроби і виражали довжину того самого відрізка, необхідно і достатньо, щоб виконувалася рівність .

Доказ цієї теореми ми опускаємо.

Два дроби і називаються рівними, якщо .

Якщо дроби дорівнюють, то пишуть .

Наприклад, так як , а , тому що , а і .

Зі сформульованих вище теореми та визначення випливає, що два дроби рівні тоді і тільки тоді, коли вони виражають довжину одного і того ж відрізка.

Нам відомо, що відношення рівності дробів є рефлексивним, симетричним і транзитивним, тобто. є ставленням еквівалентності.

З визначення рівних дробів випливає основна властивість дробу. Нагадаємо його.

Якщо чисельник і знаменник дробу помножити аборозділити на те саме число, то вийде дріб, рівний даної.

На цій властивості засновано скорочення дробів та приведення дробів до спільному знаменнику.

Скорочення дробів - Це заміна даного дробу інший, що дорівнює даної, але з меншим чисельником і знаменником.

Якщо чисельник і знаменник дробу одночасно поділяються лише на одиницю, то дріб називають нескоротною. Наприклад, – нескоротний дріб, оскільки його чисельник і знаменник поділяються одночасно лише з одиницю, тобто D(5, 17) = 1.

Частину одиниці або кілька її частин називають простим або звичайним дробом. Кількість рівних частин, куди ділиться одиниця, називається знаменником, а кількість взятих частин - чисельником. Дроб записується у вигляді:

У даному випадкуа – чисельник, b – знаменник.

Якщо чисельник менший за знаменник, то дрібок менше 1 і називається правильним дробом. Якщо чисельник більший за знаменник, то дріб більше 1, тоді дріб називається неправильним.

Якщо чисельник і знаменник дробу дорівнюють, то дріб дорівнює.

1. Якщо чисельник можна розділити на знаменник, то цей дріб дорівнює частці від поділу:

Якщо поділ виконується з залишком, то цей неправильний дріб може бути представлений змішаним числом, наприклад:

Тоді 9 - неповне приватне ( ціла частиназмішаного числа),
1 - залишок (числитель дробової частини),
5 – знаменник.

Щоб звернути змішане число в дріб, необхідно помножити цілу частину змішаного числа на знаменник і додати чисельник дробової частини.

Отриманий результат буде чисельником звичайного дробу, а знаменник залишиться тим самим.

Дії з дробами

Розширення дробу.Значення дробу не змінюється, якщо помножити його чисельник і знаменник на те саме число, відмінне від нуля.
Наприклад:

Скорочення дробу.Значення дробу не змінюється, якщо розділити її чисельник і знаменник одне й те число, відмінне від нуля.
Наприклад:

Порівняння дробів.З двох дробів з однаковими чисельникамита більша, знаменник якої менший:

З двох дробів з однаковими знаменникамита більша, чисельник якої більший:

Для порівняння дробів, у яких чисельники та знаменники різні, необхідно розширити їх, тобто привести до спільного знаменника. Розглянемо, наприклад, такі дроби:

Складання та віднімання дробів.Якщо знаменники дробів однакові, то щоб скласти дроби, необхідно скласти їх чисельники, а щоб відняти дроби, треба відняти їх чисельники. Отримана сума чи різницю буде чисельником результату, а знаменник залишиться тим самим. Якщо знаменники дробів різні, спочатку необхідно привести дроби до спільного знаменника. При додаванні змішаних чисел їх цілі та дробові частини складаються окремо. При відніманні змішаних чисел спочатку необхідно перетворити їх на вигляд неправильних дробів, потім відняти з однієї іншу, а потім знову привести результат, якщо потрібно до виду змішаного числа.

Розмноження дробів. Для перемноження дробів необхідно перемножити окремо їх чисельники та знаменники та розділити перший твір на другий.

Розподіл дробів. Для того, щоб розділити деяке число на дріб, необхідно помножити це число на дріб.

Десятковий дріб- це результат розподілу одиниці на десять, сто, тисячу тощо. частин. Спочатку пишеться ціла частина числа, потім праворуч ставиться десяткова точка. Перша цифра після десяткової точки означає число десятих, друга – число сотих, третя – число тисячних тощо. буд. Цифри, розташовані після десяткової точки, називаються десятковими знаками.

Наприклад:

Властивості десяткових дробів

Властивості:

Десятковий дріб не змінюється, якщо праворуч додати нулі: 4,5 = 4,5000.
Десятковий дріб не змінюється, якщо видалити нулі, розташовані в кінці десяткового дробу: 0,0560000 = 0,056.
Десятковий дріб зростає в 10, 100, 1000 і т.д. разів, якщо перенести десяткову точку на одну, дві, три тощо. позиції вправо: 4,5 45 (дроб зріс у 10 разів).
Десятковий дріб зменшується в 10, 100, 1000 і т.д. разів, якщо перенести десяткову точку на одну, дві, три тощо. позиції вліво: 4,5 0,45 (дроб зменшився в 10 разів).

Періодична десяткова дріб містить групу цифр, що нескінченно повторюється, звану періодом: 0,321321321321…=0,(321)

Дії з десятковими дробами

Додавання і віднімання десяткових дробів виконуються так само, як і додавання і віднімання цілих чисел, необхідно тільки записати відповідні десяткові знаки один під одним.
Наприклад:

Умноження десяткових дробів проводиться у кілька етапів:

Перемножуємо десяткові дроби як цілі числа, не зважаючи на десяткову точку.
Застосовується правило: кількість десяткових знаків у творі дорівнює сумі десяткових знаків у всіх співмножниках.

Наприклад:

Сума чисел десяткових знаків у співмножниках дорівнює: 2+1=3. Тепер необхідно з кінця числа, що вийшло, відрахувати 3 знаки і поставити десяткову точку: 0,675.

Розподіл десяткових дробів. Розподіл десяткового дробу на ціле число: якщо ділене менше від дільника, тоді потрібно записати нуль у цілій частині приватного і поставити після нього десяткову точку. Потім, не беручи до уваги десяткову точку ділимого, приєднати до цілої частини наступну цифру дробової частини і знову порівняти отриману цілу частину ділимого з дільником. Якщо нове число знову менше від дільника, треба повторити операцію. Цей процес повторюється до того часу, поки отримане ділене стане більше дільника. Після цього поділ виконується як для цілих чисел. Якщо ділене більше дільника або дорівнює йому, спочатку ділимо його цілу частину, записуємо результат поділу в приватному та ставимо десяткову точку. Після цього розподіл продовжується, як у разі цілих чисел.

Розподіл одного десяткового дробу в інший: спочатку переносяться десяткові крапки в ділимому і дільнику на число десяткових знаків у дільнику, тобто робимо дільник цілим числом, і виконуються дії, описані вище.

Для того, щоб звернути десятковий дрібу звичайну, необхідно як чисельник взяти число, що стоїть після десяткової точки, а як знаменник взяти k-у ступінь десяти (k - кількість десяткових знаків). Відмінна від нуля ціла частина зберігається у звичайному дробі; нульова ціла частина опускається.
Наприклад:

Щоб звернути звичайну дріб у десятковий, треба розділити чисельник на знаменник відповідно до правил поділу.

Відсоток – це сота частина одиниці, наприклад: 5% означає 0,05. Відношення - це окреме від розподілу одного числа на інше. Пропорція – це рівність двох відносин.

Наприклад:

Основна властивість пропорції: добуток крайніх членів пропорції дорівнює добутку її середніх членів, тобто 5х30 = 6х25. Дві взаємно залежні величини називаються пропорційними, якщо відношення їх величин зберігається незмінним (коефіцієнт пропорційності).

Таким чином, виявлено такі арифметичні дії.
Наприклад:

Безліч раціональних чисел включає позитивні і негативні числа (цілі та дробові) і нуль. Більш точне визначення раціональних чисел, прийняте в математиці, таке: число називається раціональним, якщо воно може бути представлене у вигляді звичайного нескоротного дробу виду: де a і b цілі числа.

Для від'ємного числа абсолютна величина (модуль) - це позитивне число, що отримується від зміни його знака з "-" на "+"; для позитивного числа та нуля - саме це число. Для позначення модуля числа використовуються дві прямі риси, у яких записується це число, наприклад: |–5|=5.

Властивості абсолютної величини

Нехай дано модуль числа для якого справедливі властивості:

Одночлен - це добуток двох або кількох співмножників, кожен з яких або число, або літера, або ступінь літери: 3 х a х b. Коефіцієнтом найчастіше називають лише числовий множник. Одночлени називаються подібними, якщо вони однакові чи відрізняються лише коефіцієнтами. Ступінь одночлена – це сума показників ступенів усіх його букв. Якщо серед суми одночленів є подібні, то сума може бути приведена до більш простому вигляду: 3 x a x b + 6 x a = 3 x a x (b + 2). Ця операція називається приведенням таких членів або винесенням за дужки.

Багаточлен - це сума алгебри одночленів. Ступінь багаточлена є найбільшою зі ступенів одночленів, що входять до цього багаточлена.

Існують наступні формулискороченого множення:

Методи розкладання на множники:

Алгебраїчна дріб - це вираз виду , де A і B можуть бути числом, одночлен, багаточлен.

Якщо два вирази (числові та буквені) з'єднані знаком «=», то кажуть, що вони утворюють рівність. Будь-яка правильна рівність, справедлива при всіх допустимих числових значеннях букв, що входять до нього, називається тотожністю.

Рівняння - це буквене рівність, яке справедливе за певних значень входять до нього букв. Ці букви називаються невідомими (змінними), які значення, у яких дане рівняння перетворюється на тотожність, - корінням рівняння.

Вирішити рівняння - значить знайти все його коріння. Два або кілька рівнянь називаються рівносильними, якщо вони мають одне і те ж коріння.

нуль був коренем рівняння;
рівняння мало лише кінцеве число коренів.

Основні типи рівнянь алгебри:

У лінійного рівняння ax + b = 0:

якщо a х 0 є єдиний корінь x = -b/a;
якщо a = 0, b ≠ 0, немає коріння;
якщо a = 0, b = 0, коренем є будь-яке дійсне число.

Рівняння xn = a, n N:

якщо n - непарне число, має при будь-якому дійсний корінь, рівний a / n;
якщо n – парне число, то при a 0, то має два корені.

Основні тотожні перетворення: заміна одного виразу іншим, тотожно рівним йому; перенесення членів рівняння з одного боку до іншого зі зворотними знаками; множення або розподіл обох частин рівняння на те саме вираз (число), відмінне від нуля.

Лінійним рівнянням з одним невідомим називається рівняння виду: ax+b=0 де a і b - відомі числа, а x – невідома величина.

Системи двох лінійних рівнянь із двома невідомими мають вигляд:

Де a, b, c, d, e, f – задані числа; x, y – невідомі.

Числа a, b, c, d – коефіцієнти при невідомих; e, f – вільні члени. Розв'язання цієї системи рівнянь може бути знайдено двома основними методами: метод підстановки: з одного рівняння виражаємо одне з невідомих через коефіцієнти та інше невідоме, а потім підставляємо у друге рівняння, вирішуючи останнє рівняння, знаходимо спочатку одне невідоме, потім підставляємо знайдене значення у перше рівняння і знаходимо друге невідоме; метод складання чи віднімання одного рівняння з іншого.

Операції з корінням:

Арифметичним корінням n-йступеня з неотрицательного числа a називається неотрицательное число, n-й ступіньякого дорівнює a. Алгебраїчним коренем n-го ступеняз цього числа називається безліч всіх коренів з цього числа.

Ірраціональні числа на відміну раціональних не можуть бути представлені у вигляді звичайного нескоротного дробу виду m/n, де m і n - цілі числа. Це числа нового типу, які можуть бути обчислені з будь-якою точністю, але не можуть бути замінені на раціональне число. Вони можуть з'явитися як результат геометричних вимірів, наприклад: відношення довжини діагоналі квадрата до довжини сторони дорівнює.

Квадратне рівняння є рівняння алгебри другого ступеня ax2+bx+c=0, де a, b, c - задані числові або буквені коефіцієнти, x - невідоме. Якщо розділити всі члени цього рівняння на а, то отримаємо x2+px+q=0 - наведене рівняння p=b/a, q=c/a. Його коріння знаходиться за формулою:

Якщо b2-4ac>0, тоді є два різні корені, b2- 4ac=0, тоді є два рівні корені; b2-4ac Рівняння, що містять модулі

Основні типи рівнянь, що містять модулі:
1) | f (x) | = | g (x) |;
2) | f (x) | = g(x);
3) f1(x)|g1(x)| + f2(x)|g2(x)| + … + fn (x) | gn (x) | =0, n N де f(x), g(x), fk(x), gk(x) - задані функції.

Детально розібрано основна властивість дробу, Дана його формулювання, наведено доказ і пояснювальний приклад. Також розглянуто застосування основної властивості дробу при скороченні дробів та приведенні дробів до нового знаменника.

Навігація на сторінці.

Основна властивість дробу – формулювання, доказ та пояснювальні приклади

всі звичайні дробимають один дуже важливим властивістю, Яке називають основною властивістю дробу. Сформулюємо основна властивість дробу: якщо чисельник і знаменник дробу помножити або розділити на те саме натуральне число, то вийде дріб, рівний даній.

Запишемо основну властивість дробу в буквеному вигляді: для натуральних чисел a , b і m справедливі рівність і .

Наведемо доказ основної властивості дробу. Рівності (a·m)·b=(b·m)·a та (a:m)·b=(b:m)·a справедливі в силу властивостей множення натуральних чисел та властивостей поділу натуральних чисел, тоді дроби і , а також і рівні за визначенням (дивіться рівні та нерівні дроби).

Давайте розглянемо приклад, що ілюструє основну властивість дробу. Нехай у нас є квадрат, розділений на 9 «великих» квадратів, а кожен із цих «великих» квадратів розділений на 4 «маленькі» квадрати. Таким чином, можна також говорити, що вихідний квадрат розділений на 4 · 9 = 36 «маленьких» квадратів. Зафарбуємо 5 великих квадратів. У цьому зафарбованими виявляться 4·5=20 «маленьких» квадратів. Наведемо малюнок, який відповідає нашому прикладу.

Зафарбована частина становить 5/9 вихідного квадрата, або, що те саме, 20/36 вихідного квадрата, тобто, дроби 5/9 і 20/36 рівні: або . З цих рівностей, і навіть з рівностей 20=5·4 , 36=9·4 , 20:4=5 і 36:4=9 випливає, як і .

Для закріплення розібраного матеріалу розглянемо рішення прикладу.

Чисельник і знаменник деякого звичайного дробу помножили на 62 , після чого чисельник і знаменник отриманого дробу розділили на 2 . Чи дорівнює отриманий дріб вихідним?

Примноження чисельника та знаменника дробу на будь-яке натуральне число, зокрема на 62 , дає дріб, який в силу основної властивості дробу дорівнює вихідному. Основна властивість дробу дозволяє стверджувати і те, що після поділу чисельника і знаменника отриманого дробу на 2 вийде дріб, який дорівнюватиме вихідного дробу.

так, отриманий дріб дорівнює вихідному.

Застосування основної властивості дробу

Основна властивість дробу переважно застосовується у двох випадках: по-перше, при приведенні дробів до нового знаменника, і, по-друге, при скороченні дробів.

Приведення дробу до нового знаменника – це заміна вихідного дробу, що дорівнює йому дробом, але з великим чисельником і знаменником. Для приведення дробу до нового знаменника і чисельник, і знаменник дробу множиться на деяке натуральне число, при цьому, згідно з основною властивістю дробу, виходить дріб, що дорівнює вихідному, але з іншим чисельником і знаменником. Без приведення дробів до нового знаменника не обійтися під час виконання дій зі звичайними дробами.

Основна властивість дробу дозволяє проводити скорочення дробів, і в результаті переходити від вихідного дробу до рівного їй дробу, але з меншим чисельником і знаменником. Скорочення дробу полягає у розподілі чисельника та знаменника вихідного дробу на будь-який відмінний від одиниці позитивний загальний дільник чисельника та знаменника (якщо таких спільних дільників немає, то вихідний дріб нескоротний, тобто, не підлягає скороченню). Зокрема, розподіл на найбільший спільний дільник приведе вихідний дріб до нескоротного виду.

www.cleverstudents.ru

Основна властивість дробу

Щоб порівняти, скласти або відняти звичайні дроби з різними знаменниками, їх треба спочатку призвести до одного (одного) знаменника.

Для цього число, від якого взята частина частками (кількість часток числа визначає знаменник), розбивається на більшу кількість часток так, щоб усі знаменники дробів були кратні між собою.

Наприклад, потрібно порівняти, скласти або відняти дроби та. Розглянемо малюнку дроблення на частки (1 розділили на 4 частини та 1 розділили на 2 частини), за ціле приймається 1.

Розділивши на 2 частки, отримуємо наочне порівняння.

Отже, , оскільки частки міститься 2 частки по Запишем: . За правилами арифметики: Виділимо прості множники у чисельнику та знаменнику:

Наведені малюнки дозволяють вивести правило, зване основною властивістю дробу.

Правило. Чисельник і знаменник дробу можна множити або ділити на те саме натуральне число, від чого величина дробу не змінюється.

Якщо чисельник нового дробу уявити твором (або приватним) першого дробу та будь-якого натурального числа, а знаменник нового дробу - твором (або приватним) знаменника першого дробу і того ж числа, то новий дріб зберігає при обчисленні творів (або приватних) значення (величину) вихідного дробу, тому між заданим та отриманим дробом можна ставити знак рівності.

Можна записати основна властивість дробупри множенні чисельника та знаменника дробу на число:

Можна записати основна властивість дробупри розподілі чисельника та знаменника дробу на число:

Скорочення дробів

За допомогою дробів ту саму частину цілого предмета можна записати різними способами.

На малюнку зафарбовано половину кола

Отже, всі ці дроби рівні.

Дріб

Для зручності додатковий множник записують на похилій межі праворуч над дробом.

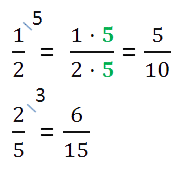
Повернемося ще раз до наших дробів та запишемо їх в іншому порядку.

Дроб, рівну даній, можна отримати, якщо чисельник і знаменник дробу одночасно розділити на те саме число, не рівне нулю.

Таке перетворення дробу називають скороченням дробу.

Скорочення дробу зазвичай записують так.

Чисельник і знаменник закреслюються рисочками, і поруч із ними записуються результати розподілу (приватні) чисельника і знаменника одне й те число.

Число, на яке ділили чисельник та знаменник, тримаємо в умі.

У прикладі ми скорочували (тобто ділили і чисельник, і знаменник) дріб на двійку, яку тримали в умі.

Скорочення дробу можна проводити послідовно.

Сформулюємо основну властивість дробу.

Якщо чисельник і знаменник дробу помножити або розділити на те саме число, не рівне нулю, то вийде дріб, рівний даній.

Запишемо цю властивість у вигляді буквених виразів.

, де "a", "b" і "k" - натуральні числа.

Основна властивість дробу. Скорочення дробів. Рівність дробів.

Рівність дробів.

Ця тема досить важлива на основних властивостях дробів заснована вся подальша математика та алгебра. Розглянуті властивості дробів, незважаючи на свою важливість, дуже прості.

Щоб зрозуміти основні властивості дробіврозглянемо коло.

На колі видно, що чотири частини або частки зафарбовані з восьми можливих. Запишемо отриманий дріб \(\frac \)

На наступному колі видно, що зафарбовано одну частину з двох можливих. Запишемо дроб, що вийшов \(\frac \)

Якщо уважно придивимося, то побачимо, що в першому випадку, що в другому випадку у нас зафарбовано половину кола, тому отримані дроби дорівнюють \(\frac = \frac \), тобто це одне й те саме число.

Як це довести математично? Дуже просто, згадаємо таблицю множення та розпишемо перший дріб на множники.

Що ми зробили? Розписали чисельник та знаменник на множники \(\frac > >\), а потім розділили дроби \(\frac \cdot \color \). Чотири поділити на чотири це 1, а одиниця помножена на будь-яке число і є саме число. Те, що ми проробили в наведеному прикладі називається скороченням дробів.

Подивимося ще один приклад і скоротимо дріб.

Ми знову розписали чисельник та знаменник на множники і однаковий числа в чисельники та знаменники скоротили. Тобто два ділене на два дало одиницю, а одиниця помножена на будь-яке число дає те саме число.

Основна властивість дробу.

Звідси випливає основна властивість дробу:

Якщо і чисельник, і знаменник дробу помножити на те саме число (крім нуля), то величина дробу не зміниться.

Також можна дроби чисельник і знаменник ділити на одне й те саме число одночасно.
Розглянемо приклад:

Якщо і чисельник, і знаменник дробу ділити на одне й те саме число (крім нуля), то величина дробу не зміниться.

Дроби у яких є і в чисельники, і в знаменники загальні прості дільники називаються скоротливими дробами.

Приклад скоротливого дробу: \(\frac , \frac , \frac , \frac , …\)

Так само є і нескоротні дроби.

Нескоротний дріб– це дріб у яких немає у чисельники та знаменники спільних простих дільників.

Приклад нескоротного дробу: \(\frac , \frac , \frac , \frac , …\)

Будь-яке число можна подати у вигляді дробу, тому що будь-яке число ділиться на одиницю,наприклад:

Запитання до теми:
Як ви думаєте, будь-яку можна дроб скоротити чи ні?
Відповідь: ні, бувають скорочені дроби та нескоротні дроби.

Перевірте чи справедливість рівність: \(\frac = \frac \)?
Відповідь: розпишемо дріб \(\frac = \frac = \frac \), Так справедливо.

Приклад №1:
а) Знайдіть дріб зі знаменником 15, рівну дробу \(\frac \).
б) Знайдіть дріб з чисельником 8, рівний дробу \(\frac \).

Рішення:
а) Нам потрібно, щоб у знаменнику стояло число 15. Зараз у знаменнику число 3. На яке число потрібно помножити цифру 3, щоб отримати 15? Згадаймо таблицю множення 3⋅5. Нам треба скористатися основною властивістю дробів і помножити і чисельник, і знаменник дробу \(\frac \)на 5.

б) Нам потрібно, щоб у чисельнику стояло число 8. Зараз у чисельнику стоїть число 1. На яке число потрібно помножити цифру 1, щоб отримати 8? Звісно, 1⋅8. Нам треба скористатися основною властивістю дробів і помножити і чисельник, і знаменник дробу \(\frac \)на 8. Отримаємо:

Приклад №2:
Знайдіть нескоротний дріб, рівний дробу: а) \(\frac \),б) \(\frac \).

Приклад №3:
Запишіть число у вигляді дробу: а) 13 б)123

Урок на тему рівність дробів, 5 клас, підручник Микільський С. М. та ін.

Встигніть скористатися знижками до 50% на курси «Інфоурок»

Нагадуємо, що відповідно до профстандарту педагога (затверджений Наказом Мінпраці Росії), якщо у Вас немає відповідного предмета освіти, що викладається, то Вам необхідно пройти професійну перепідготовку за профілем педагогічної діяльності. Зробити це Ви можете дистанційно на сайті проекту «Інфоурок» та отримати диплом із присвоєнням кваліфікації вже через 2 місяці!

Тільки зараз діє ЗНИЖКА 50%для всіх освітян на всі 111 курсів професійної перепідготовки! Доступна розстрочка з першим внеском лише 10%, при цьому ціна курсу не збільшується через використання розстрочки!

Картка для практичної роботи.docx

Картка 1

Картка 2

Завдання.Подивіться малюнки і зробіть висновок про рівність дробів.

Підказка 1. Яка частина кіл та квадратів зафарбована?

Підказка 1. Запишіть дроби, які позначають зафарбовану частину кожної фігури.

Підказка 2. Зробіть висновок про рівність отриманих дробів.

Вибраний для перегляду документ Технологічна картауроку математики в 5 класі.

Технологічна карта уроку математики у 5 класі

Тема уроку: «Рівність дробів» (підручник «Математика 5», Микільський С. М., Потапов М. К. та ін.)

Цілі (завдання) уроку:

— познайомити учнів з основною властивістю дробу, показати його застосування для скорочення дробів;

- вчити скорочувати дроби та визначати нескоротні;

— розвивати вміння застосовувати математичні знання на вирішення практичних завдань;

- виховувати культуру поведінки при груповий роботі;

- Виховувати інтерес до предмета.

- знати основну властивість дробу, визначення скорочення дробів та нескоротного дробу;

- вміти приводити дроби до нового знаменника, скорочувати дроби;

розуміти сенс поставленого завдання; ініціатива, винахідливість, активність під час вирішення математичних завдань;

- Вміння бачити математичне завданняу контексті проблемної ситуації;

— розуміння сутності алгоритмічних розпоряджень та вміння діяти відповідно до запропонованого алгоритму.

Тип уроку, педагогічна технологія

Вивчення нового, технології проблемного діалогу.

Дошка, крейда, комп'ютер з мультимедійним проектором, інтерактивна дошка, роздаткові матеріали, ролик з фізкультхвилинкою, листи самооцінки

Опорні поняття, терміни

Нові поняття та зв'язки між ними

Скоротний дріб, нескоротний дріб

Контроль, самоконтроль на уроці

Використовувані методи, прийоми, форми

Універсальні навчальні дії

I. Організаційний момент.

Зошити ви отримали на перерві, оскільки домашнє завданнявсі виконали і питань щодо нього не виникло.

Вияв доброзичливої уваги.

Перевірка наявності навчальних засобів, раціональне розміщення на парті

Взаємне вітання, контроль присутніх, перевірка готовності кабінету до уроку.

Готовність учнів до навчання, діяльності

II. Актуалізація знань

Згадаймо те, що ми вивчали на минулих уроках. Що ми вивчали? (Дроби)

1. Що записується під межею дробу?

2. Що він показує?

3. Що записується над межею дробу?

4. Що він показує?

5. Яку дію замінює характеристика дробу?

6. Знайти ¼ від 120.

(На скільки частин розділили ціле)

(скільки таких частин взяли)

Тестові завдання, відповіді надаються за допомогою сигналів різного кольору

Регулятивні:вольова саморегуляція.

Особистісні : дія смислоутворення, мотивація вчення

планування навчального співробітництва з учителем та з однолітками.

Готовність до відкриття нового

III . Постановка проблеми

Зараз я пропоную вам вирішити таке завдання-казку. Проблемне завдання

У деякому царстві, у деякій державі жив – був цар, і мав трьох синів. Ось якось скликав він своїх синів і каже: “Синочки ви мої милі, видно, настав мені час йти на спокій. Зібрав я вас, щоб поділити між вами спадщину, наше царство – державу. Та ось біда – вчені наші видно щось наплутали. Тобі, старший мій сину, відписано нашої держави, тобі, середній мій сину, — а тобі, мій молодший — ”. Обурився молодший син: “За що мене обділили?” І посварилися брати між собою. А цар видав указ “Хто зможе помилку знайти і синів моїх помирити, того чекає царська нагорода. ”

Хлопці, а ми з вами можемо помирити царя та його синів? Що нам потрібно з'ясувати?

Отже, чому, мабуть, ми навчатимемося на сьогоднішньому уроці?

І спробуймо сформулювати тему нашого уроку.

Відкрийте свої зошити, підпишіть у них число, класну роботу та тему уроку «Рівність дробів».

(Рівні дроби чи ні)

(Дізнаватись, рівні дроби чи ні)

формулювання мети уроку

Постановка проблеми, формулювання мети, теми уроку

IV. Планування вирішення навчальної задачі

А зараз допоможіть мені скласти план уроку, тобто визначити те, чим ми займатимемося.

(1. Навчитися визначати, чи рівні дроби чи ні).

Регулятивні:планування пізнавальної діяльності

Складання плану уроку

Стародавня китайська приказка говорить: «Я чую і забуваю, бачу і запам'ятовую, роблю і розумію». І щоб зрозуміти тему сьогоднішнього уроку, проведемо практичну роботу.

Кожен із вас на столі лежать картки.

Візьміть картку 1.

Попрацюємо із квадратом. Розділіть квадрат на чотири рівні частини та зафарбуйте три з них. Яка частина

квадрата виявилася зафарбованою?

Кожну чверть квадрата поділіть на 4 частини. На скільки частин тепер

А скільки таких частин у трьох зафарбованих чвертях квадрата?

Яку частину квадрата зафарбовано?

Що ж ви можете сказати про дроби? і 12/16?

Візьміть картку 2 та дайте відповідь на запитання:

1. Яка частина від цілого зображена та зафарбована на малюнках? Підпишіть під кожним колом, яку його частину зафарбовано.

Що ви можете сказати про ці дроби?

Отже, ту саму частину можна записати по-різному.

Давайте уважно подивимося на ці дроби. Як можна з одного дробу отримати інший, наприклад, як з ¾ отримати 12/16?

А як з 4/8 отримати 2/4,?

Робимо висновок, формулюємо правило:

Хлопці, властивість, яку ми з вами зараз сформулювали, дуже важлива і називається вона основною властивістю дробу.

Запишіть, будь ласка, з дошки правило та формули.

a, b, c – натуральні. Зверніть на це увагу, це дуже важливо, тому що на 0 ділити не можна.

(помножити чисельник та знаменник на 4)

(Поділити чисельник та знаменник на 2, на 4)

(При множенні та розподілі чисельника та знаменника дробу на те саме число (крім 0) її величина не зміниться .)

Пізнавальні:порівняння, узагальнення, формулювання висновку

Виконання практичної роботи. Формулювання основної властивості дробу

VI . Формування способу дії

Подайте такі дроби: у вигляді дробу зі знаменником 12.

Подайте такі дроби: у вигляді дробу із знаменником 3.

Письменно: замініть дроби рівними їм дробами із меншими знаменниками. Хлопці, перетворення, яке ми з вами щойно виконували, називається скороченням дробів.

Запишіть із екрана, що таке скорочення дробу.

Розділити чисельник і знаменник одного дробу на те саме число, значить скоротити її.

Якщо чисельник та знаменник дробу не мають спільних простих дільників, то цей дріб називається нескоротною.

Виконують завдання. Записують у зошиті, що таке скорочення дробів і що таке нескоротний дріб

Регулятивні:корекція дій та результатів

Первинне засвоєння та застосування основної властивості дробу, визначення скорочення дробів, нескоротного дробу

VII . Формування нових знань та способів дії

Повернімося до плану нашого уроку. Що ми зробили? Що ще потрібно зробити?

Чудово. Зараз я пропоную вам трохи пограти.

Об'єднаємось у дві групи. Перша група (I ряд) із усіх запропонованих дробів

вибере дроби, що дорівнюють 1/2, а друга група (II ряд) — дроби, що дорівнюють 1/3.

А тепер перевіримо, як ви впоралися із завданням.

Тепер повернемося до казкового завдання, яке викликало у нас труднощі на початку уроку. Скажіть, тепер ви можете відповісти на запитання: чи наплутали щось радники царя?

А зараз ще трохи потренуємось. Візьміть у руки листочки з тренувальними вправами, уважно прочитайте завдання та виконуйте їх.

(Навчилися визначати, чи дорівнюють дроби. Потрібно потренуватися)

(Тепер можемо. Спадщину поділили порівну, тому що представлені дроби рівні)

Тренувальні вправи на картках

Робота з інтерактивною дошкою. Робота у групах

Комунікативні:визначення цілей та функцій учасників у групі; ініціативне співробітництво; контроль, корекція, оцінка дій партнера.

Застосування та відпрацювання нових знань та способів дії

VIII . Підведення підсумків уроку, рефлексія, домашнє завдання

Щоб зрозуміти основні властивості дробіврозглянемо коло.

На колі видно, що 4 частини або зафарбовані із восьми можливих. Запишемо отриманий дріб \(\frac(4)(8)\)

На наступному колі видно, що зафарбовано одну частину з двох можливих. Запишемо дроб, що вийшов \(\frac(1)(2)\)

Якщо уважно придивимося, то побачимо, що в першому випадку, що в другому випадку у нас зафарбовано половину кола, тому отримані дроби дорівнюють \(\frac(4)(8) = \frac(1)(2)\), тобто це те саме число.

Як це довести математично? Дуже просто, згадаємо таблицю множення та розпишемо перший дріб на множники.

\(\frac(4)(8) = \frac(1 \cdot \color(red) (4))(2 \cdot \color(red) (4)) = \frac(1)(2) \cdot \color(red) (\frac(4)(4)) =\frac(1)(2) \cdot \color(red)(1) = \frac(1)(2)\)

Що ми зробили? Розписали чисельник і знаменник на множники \(\frac(1 \cdot \color(red) (4))(2 \cdot \color(red) (4))\), а потім розділили дроби \(\frac(1) (2) \cdot \color(red) (\frac(4)(4))\). Чотири поділити на чотири це 1, а одиниця помножена на будь-яке число і є саме число. Те, що ми проробили в наведеному прикладі називається скороченням дробів.

Подивимося ще один приклад і скоротимо дріб.

\(\frac(6)(10) = \frac(3 \cdot \color(red) (2))(5 \cdot \color(red) (2)) = \frac(3)(5) \cdot \color(red) (\frac(2)(2)) =\frac(3)(5) \cdot \color(red)(1) = \frac(3)(5)\)

Основна властивість дробу.

Звідси випливає основна властивість дробу:

Якщо і чисельник, і знаменник дробу помножити на те саме число (крім нуля), то величина дробу не зміниться.

\(\bf \frac(a)(b) = \frac(a \cdot n)(b \cdot n)\)

Також можна дроби чисельник і знаменник ділити на одне й те саме число одночасно.
Розглянемо приклад:

\(\frac(6)(8) = \frac(6 \div \color(red) (2))(8 \div \color(red) (2)) = \frac(3)(4)\)

Якщо і чисельник, і знаменник дробу ділити на одне й те саме число (крім нуля), то величина дробу не зміниться.

\(\bf \frac(a)(b) = \frac(a \div n)(b \div n)\)

Дроби у яких є і в чисельники, і в знаменники загальні прості дільники називаються скоротливими дробами.

Приклад скоротливого дробу: \(\frac(2)(4), \frac(6)(10), \frac(9)(15), \frac(10)(5), …\)

Так само є і нескоротні дроби.

Нескоротний дріб– це дріб у яких немає у чисельники та знаменники спільних простих дільників.

Приклад нескоротного дробу: \(\frac(1)(2), \frac(3)(5), \frac(5)(7), \frac(13)(5), ...\)

Будь-яке число можна подати у вигляді дробу, тому що будь-яке число ділиться на одиницю,наприклад:

\(7 = \frac(7)(1)\)

Перевірте чи справедливість рівність: \(\frac(7)(11) = \frac(14)(22)\)?
Відповідь: розпишемо дріб \(\frac(14)(22) = \frac(7 \cdot 2)(11 \cdot 2) = \frac(7)(11)\), Так справедливо.

Приклад №1:
а) Знайдіть дріб із знаменником 15, рівний дробу \(\frac(2)(3)\).
б) Знайдіть дріб з чисельником 8, рівний дробу \(\frac(1)(5)\).

\(\frac(2)(3) = \frac(2 \cdot 5)(3 \cdot 5) = \frac(10)(15)\)

\(\frac(1)(5) = \frac(1 \cdot 8)(5 \cdot 8) = \frac(8)(40)\)

Приклад №2:
Знайдіть нескоротний дріб, рівний дробу: а) \(\frac(16)(36)\),б) \(\frac(10)(25)\).

Рішення:
а) \(\frac(16)(36) = \frac(4 \cdot 4)(9 \cdot 4) = \frac(4)(9)\)

б) \(\frac(10)(25) = \frac(2 \cdot 5)(5 \cdot 5) = \frac(2)(5)\)

Приклад №3:
Запишіть число у вигляді дробу: а) 13 б)123

Рішення:
а) \(13 = \frac(13) (1)\)

б) \(123 = \frac(123) (1)\)

Дії з дробами регулюються основною властивістю дробу: якщо чисельник і знаменник дробу помножити або розділити на те саме натуральне число, то вийде рівний їй дріб.

2/5 = 4/10, т.к. 2 ∙ 2/5 ∙ 2

Рівні дроби насправді є записом однієї й тієї числа.

Порівняємо, 2/5 = 0,4 та 4/10 = 0,4.

Числа, які ми можемо записати у вигляді дробів, називаються раціональними числами, множина яких позначається латинською літерою Q. Згадаємо, що будь-яке ціле число ми можемо записати у вигляді дробу: 4 = 4/1, отже, будь-яке ціле число раціонально. Інакше кажучи, безліч цілих чисел Z – це підмножина Q, чи Z належить Q.

Отже, помножимо дріб на 5: 1/5 ∙ 5 = 1 ∙ 5/5 ∙ 5 = 5/25.

Розділимо дріб на 3: 33/21: 3 = 33: 3/21: 3 = 11/7 = 14/7.

Примноження чисельника та знаменника дробу на те саме число називається приведення дробу до знаменника.

Наприклад: якщо дріб 3/4 ми помножимо на 2 і отримаємо 6/8, ми скажемо, що ми привели дріб 3/4 до знаменника 8, причому число 2 називається додатковим множником.

Наведемо дріб 4/5 до знаменника 30.

1. Знайдемо додатковий множник: 30: 5 = 6. Отже наш додатковий множник 6.

2. Помножимо чисельник і знаменник дробу на 6: 4 ∙ 6/5 ∙ 6 = 24/30.

Отже, наш дріб 24/30.

Ґрунтуючись на головній властивості дробу, ми приходимо до поняття «скорочення дробу». Скороченням дробу називається розподіл чисельника та знаменника дробу на їхній спільний дільник (відмінний від одиниці).

Розглянемо дріб 15/20. Число 5 для чисел 15 та 20 є спільним дільником. Отже, і чисельник, і знаменник дробу можна поділити на спільний дільник дробу 5. Отримаємо: 15: 5/20: 5 = 3/4.

Найбільшим загальним дільником називається найбільше число, яке можна скоротити дріб. Наприклад, дріб 30/45 можна скоротити на 3 та 5, але найбільшим числом, на яку можна скоротити наш дріб, є число 15: 30: 15 / 45: 15 = 2/3.

Буває так, що чисельник і знаменник дробу немає спільних дільників, крім одиниці; такий дріб ми називаємо нескоротним, а числа, які мають спільних дільників, крім одиниці, називають взаємно простими.

Приведення дробів до спільного знаменника дозволяє порівнювати дроби з різними знаменниками. Іншими словами, щоб порівняти дроби з різними знаменниками, необхідно:

1. привести дроби до спільного знаменника;
2. порівняти чисельники дробів, що вийшли.

Розглянемо приклад 3/5??? 4/7.

1. Приведемо дроби до спільного знаменника 35. Для цього домножимо перший дріб на 7 (і чисельник, і знаменник), а другий (і чисельник, і знаменник) на 5. Отримаємо: 21/35 ??? 20/35.

2. Порівняємо чисельники дробів, що вийшли: 21 більше 20, отже, 3/5 > 4/7.

Розглянемо приклад: 6/9??? 8/12.

Загальним знаменником наших дробів буде число 9 ∙ 12. Але щоб полегшити рішення прикладу, потрібно помітити, що наші дроби можна скоротити (6/9 на 3, 8/12 на 4): 2/3 ??? 2/3, тобто. 2/3 = 2/3, отже, 6/9 = 8/12. Як бачимо, у такому разі нам знадобилося набагато менше часу на встановлення рівності дробів.